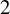For any prime p and S a p-group isomorphic to a Sylow p-subgroup of a rank $2$ simple group of Lie type in characteristic p, we determine all saturated fusion systems supported on S up to isomorphism.

A group $G=AB$ is the weakly mutually permutable product of the subgroups A and B, if A permutes with every subgroup of B containing $A \cap B$ and B permutes with every subgroup of A containing $A \cap B$. Weakly mutually permutable products were introduced by the first, second and fourth authors [‘Generalised mutually permutable products and saturated formations’, J. Algebra 595 (2022), 434–443] who showed that if $G'$ is nilpotent, A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then $G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $, where $ \mathfrak {F} $ is a saturated formation containing $ \mathfrak {U} $, the class of supersoluble groups. In this article we prove results on weakly mutually permutable products concerning $ \mathfrak {F} $-residuals, $ \mathfrak {F} $-projectors and $\mathfrak {F}$-normalisers. As an application of some of our arguments, we unify some results on weakly mutually $sn$-products.

In this paper, we investigate finite solvable tidy groups. We prove that a solvable group with order divisible by at least two primes is tidy if all of its Hall subgroups that are divisible by only two primes are tidy.

To each pair consisting of a saturated fusion system over a p-group together with a compatible family of Külshammer-Puig cohomology classes, one can count weights in a hypothetical block algebra arising from these data. When the pair arises from a genuine block of a finite group algebra in characteristic p, the number of conjugacy classes of weights is supposed to be the number of simple modules in the block. We show that there is unique such pair associated with each Benson-Solomon exotic fusion system, and that the number of weights in a hypothetical Benson-Solomon block is $12$ , independently of the field of definition. This is carried out in part by listing explicitly up to conjugacy all centric radical subgroups and their outer automorphism groups in these systems.

For a finite abelian p-group A and a subgroup $\Gamma \le \operatorname {\mathrm {Aut}}(A)$, we say that the pair $(\Gamma ,A)$ is fusion realizable if there is a saturated fusion system ${\mathcal {F}}$ over a finite p-group $S\ge A$ such that $C_S(A)=A$, $\operatorname {\mathrm {Aut}}_{{\mathcal {F}}}(A)=\Gamma $ as subgroups of $\operatorname {\mathrm {Aut}}(A)$, and . In this paper, we develop tools to show that certain representations are not fusion realizable in this sense. For example, we show, for $p=2$ or $3$ and $\Gamma $ one of the Mathieu groups, that the only ${\mathbb {F}}_p\Gamma $-modules that are fusion realizable (up to extensions by trivial modules) are the Todd modules and in some cases their duals.

A classical result of Baer states that a finite group G which is the product of two normal supersoluble subgroups is supersoluble if and only if Gʹ is nilpotent. In this article, we show that if G = AB is the product of supersoluble (respectively, w-supersoluble) subgroups A and B, A is normal in G and B permutes with every maximal subgroup of each Sylow subgroup of A, then G is supersoluble (respectively, w-supersoluble), provided that Gʹ is nilpotent. We also investigate products of subgroups defined above when $ A\cap B=1 $ and obtain more general results.

We state a sufficient condition for a fusion system to be saturated. This is then used to investigate localities with kernels: that is, localities that are (in a particular way) extensions of groups by localities. As an application of these results, we define and study certain products in fusion systems and localities, thus giving a new method to construct saturated subsystems of fusion systems.

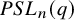Let q be a nontrivial odd prime power, and let $n \ge 2$ be a natural number with $(n,q) \ne (2,3)$ . We characterize the groups $PSL_n(q)$ and 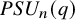$PSU_n(q)$ by their 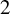$2$ -fusion systems. This contributes to a programme of Aschbacher aiming at a simplified proof of the classification of finite simple groups.

In this note, we investigate some products of subgroups and vanishing conjugacy class sizes of finite groups. We prove some supersolubility criteria for groups with restrictions on the vanishing conjugacy class sizes of their subgroups.

Let $\pi $ be a set of primes. We say that a group G satisfies $D_{\pi }$ if G possesses a Hall $\pi $ -subgroup H and every $\pi $ -subgroup of G is contained in a conjugate of H. We give a new $D_{\pi }$ -criterion following Wielandt’s idea, which is a generalisation of Wielandt’s and Rusakov’s results.

We show that the automorphism group of a linking system associated to a saturated fusion system $\mathcal {F}$ depends only on $\mathcal {F}$ as long as the object set of the linking system is $\mathrm {Aut}(\mathcal {F})$ -invariant. This was known to be true for linking systems in Oliver’s definition, but we demonstrate that the result holds also for linking systems in the considerably more general definition introduced previously by the author of this article. A similar result is proved for linking localities, which are group-like structures corresponding to linking systems. Our argument builds on a general lemma about the existence of an extension of a homomorphism between localities. This lemma is also used to reprove a theorem of Chermak showing that there is a natural bijection between the sets of partial normal subgroups of two possibly different linking localities over the same fusion system.

In this paper, we study the structure of finite groups $G=AB$ which are a weakly mutually $sn$ -permutable product of the subgroups A and B, that is, A permutes with every subnormal subgroup of B containing $A \cap B$ and B permutes with every subnormal subgroup of A containing $A \cap B$ . We obtain generalisations of known results on mutually $sn$ -permutable products.

We show that if w is a multilinear commutator word and G a finite group in which every metanilpotent subgroup generated by w-values is of rank at most r, then the rank of the verbal subgroup $w(G)$ is bounded in terms of r and w only. In the case where G is soluble, we obtain a better result: if G is a finite soluble group in which every nilpotent subgroup generated by w-values is of rank at most r, then the rank of $w(G)$ is at most $r+1$ .

A rigid automorphism of a linking system is an automorphism that restricts to the identity on the Sylow subgroup. A rigid inner automorphism is conjugation by an element in the center of the Sylow subgroup. At odd primes, it is known that each rigid automorphism of a centric linking system is inner. We prove that the group of rigid outer automorphisms of a linking system at the prime $2$ is elementary abelian and that it splits over the subgroup of rigid inner automorphisms. In a second result, we show that if an automorphism of a finite group G restricts to the identity on the centric linking system for G, then it is of $p'$-order modulo the group of inner automorphisms, provided G has no nontrivial normal $p'$-subgroups. We present two applications of this last result, one to tame fusion systems.

It is known that there exists a first-order sentence that holds in a finite group if and only if the group is soluble. Here it is shown that the corresponding statements with ‘solubility’ replaced by ‘nilpotence’ and ‘perfectness’, among others, are false.

These facts present difficulties for the study of pseudofinite groups. However, a very weak form of Frattini’s theorem on the nilpotence of the Frattini subgroup of a finite group is proved for pseudofinite groups.

Denote by m(G) the largest size of a minimal generating set of a finite group G. We estimate m(G) in terms of $\sum _{p\in \pi (G)}d_p(G),$ where we are denoting by dp(G) the minimal number of generators of a Sylow p-subgroup of G and by π(G) the set of prime numbers dividing the order of G.

Let $\mathfrak{F}$ be a class of finite groups and $G$ a finite group. Let ${\mathcal{L}}_{\mathfrak{F}}(G)$ be the set of all subgroups $A$ of $G$ with $A^{G}/A_{G}\in \mathfrak{F}$. A chief factor $H/K$ of $G$ is $\mathfrak{F}$-central in $G$ if $(H/K)\rtimes (G/C_{G}(H/K))\in \mathfrak{F}$. We study the structure of $G$ under the hypothesis that every chief factor of $G$ between $A_{G}$ and $A^{G}$ is $\mathfrak{F}$-central in $G$ for every subgroup $A\in {\mathcal{L}}_{\mathfrak{F}}(G)$. As an application, we prove that a finite soluble group $G$ is a PST-group if and only if $A^{G}/A_{G}\leq Z_{\infty }(G/A_{G})$ for every subgroup $A\in {\mathcal{L}}_{\mathfrak{N}}(G)$, where $\mathfrak{N}$ is the class of all nilpotent groups.

We finish the classification, begun in two earlier papers, of all simple fusion systems over finite nonabelian p-groups with an abelian subgroup of index p. In particular, this gives many new examples illustrating the enormous variety of exotic examples that can arise. In addition, we classify all simple fusion systems over infinite nonabelian discrete p-toral groups with an abelian subgroup of index p. In all of these cases (finite or infinite), we reduce the problem to one of listing all 𝔽pG-modules (for G finite) satisfying certain conditions: a problem which was solved in the earlier paper [15] using the classification of finite simple groups.

Suppose that $G$ is a finite group and $H$ is a subgroup of $G$. $H$ is said to be $s$-semipermutable in $G$ if $H{{G}_{p}}\,=\,{{G}_{p}}H$ for any Sylow $p$-subgroup ${{G}_{p}}$ of $G$ with $\left( p,\,\left| H \right| \right)\,=\,1$; $H$ is said to be $s$-quasinormally embedded in $G$ if for each prime $p$ dividing the order of $H$, a Sylow $p$-subgroup of $H$ is also a Sylow $p$-subgroup of some $s$-quasinormal subgroup of $G$. In every non-cyclic Sylow subgroup $P$ of $G$ we fix some subgroup $D$ satisfying $1\,<\,\left| D \right|\,<\,\left| P \right|$ and study the structure of $G$ under the assumption that every subgroup $H$ of $P$ with $\left| H \right|\,=\,\left| D \right|$ is either $s$-semipermutable or $s$-quasinormally embedded in $G$. Some recent results are generalized and unified.