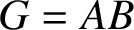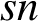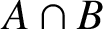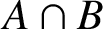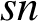1 Introduction
All groups considered here will be finite.
Mutually permutable products, that is, products
![]() $G=AB$
such that A permutes with every subgroup of B and B permutes with every subgroup of A, have been extensively studied by many authors [Reference Ballester-Bolinches, Esteban-Romero and Asaad3]. In recent years, some other permutability connections between the factors have also been considered. In particular, the rich normal structure of a mutually permutable product of two nilpotent groups [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Ch. 5] has motivated interest in the study of mutually
$G=AB$
such that A permutes with every subgroup of B and B permutes with every subgroup of A, have been extensively studied by many authors [Reference Ballester-Bolinches, Esteban-Romero and Asaad3]. In recent years, some other permutability connections between the factors have also been considered. In particular, the rich normal structure of a mutually permutable product of two nilpotent groups [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Ch. 5] has motivated interest in the study of mutually
![]() $sn$
-permutable products.
$sn$
-permutable products.
Definition 1.1. We say that a group
![]() $G = AB$
is the mutually
$G = AB$
is the mutually
![]() $sn$
-permutable product of the subgroups A and B if A permutes with every subnormal subgroup of B and B permutes with every subnormal subgroup of A.
$sn$
-permutable product of the subgroups A and B if A permutes with every subnormal subgroup of B and B permutes with every subnormal subgroup of A.
Carocca [Reference Carocca5] showed that a mutually
![]() $sn$
-permutable product of two soluble groups is also soluble. In [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1], the authors analyse the structure of mutually
$sn$
-permutable product of two soluble groups is also soluble. In [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1], the authors analyse the structure of mutually
![]() $sn$
-permutable products and prove the following extension of a classical result of Asaad and Shaalan [Reference Asaad and Shaalan2].
$sn$
-permutable products and prove the following extension of a classical result of Asaad and Shaalan [Reference Asaad and Shaalan2].
Theorem 1.2 [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1, Theorem B]
Let
![]() $G = AB$
be the mutually
$G = AB$
be the mutually
![]() $sn$
-permutable product of the subgroups A and B, where A is supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is supersoluble.
$sn$
-permutable product of the subgroups A and B, where A is supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is supersoluble.
Following [Reference Valisev, Valiseva and Tyutyanov8], we say that a subgroup H of a group G is
![]() $\mathbb {P}$
-subnormal in G whenever either
$\mathbb {P}$
-subnormal in G whenever either
![]() $H=G$
or there exists a chain of subgroups
$H=G$
or there exists a chain of subgroups
![]() $H=H_{0} \leq H_{1} \leq \cdots \leq H_{n-1} \leq H_{n}=G$
such that
$H=H_{0} \leq H_{1} \leq \cdots \leq H_{n-1} \leq H_{n}=G$
such that
![]() $| H_{i} : H_{i-1} |$
is a prime for every
$| H_{i} : H_{i-1} |$
is a prime for every
![]() $i=1, \dots , n$
. It turns out that supersoluble groups are exactly those groups in which every subgroup is
$i=1, \dots , n$
. It turns out that supersoluble groups are exactly those groups in which every subgroup is
![]() $\mathbb {P}$
-subnormal. Having in mind this result and the influence of the embedding of Sylow subgroups on the structure of a group, the following extension of the class of supersoluble groups introduced in [Reference Valisev, Valiseva and Tyutyanov8] seems to be natural.
$\mathbb {P}$
-subnormal. Having in mind this result and the influence of the embedding of Sylow subgroups on the structure of a group, the following extension of the class of supersoluble groups introduced in [Reference Valisev, Valiseva and Tyutyanov8] seems to be natural.
Definition 1.3. A group G is called widely supersoluble, w-supersoluble for short, if every Sylow subgroup of G is
![]() $\mathbb {P}$
-subnormal in G.
$\mathbb {P}$
-subnormal in G.
The class of all finite
![]() $ w $
-supersoluble groups, denoted by
$ w $
-supersoluble groups, denoted by
![]() $ w\mathcal {U} $
, is a saturated formation of soluble groups containing
$ w\mathcal {U} $
, is a saturated formation of soluble groups containing
![]() $ \mathcal {U} $
, the class of all supersoluble groups, which is locally defined by a formation function f, such that for every prime p,
$ \mathcal {U} $
, the class of all supersoluble groups, which is locally defined by a formation function f, such that for every prime p,
![]() $f(p)$
is composed of all soluble groups G whose Sylow subgroups are abelian of exponent dividing
$f(p)$
is composed of all soluble groups G whose Sylow subgroups are abelian of exponent dividing
![]() $p-1$
[Reference Valisev, Valiseva and Tyutyanov8, Theorems 2.3 and 2.7]. Not every group in
$p-1$
[Reference Valisev, Valiseva and Tyutyanov8, Theorems 2.3 and 2.7]. Not every group in
![]() $w\mathcal {U}$
is supersoluble [Reference Valisev, Valiseva and Tyutyanov8, Example 1]. However, every group in
$w\mathcal {U}$
is supersoluble [Reference Valisev, Valiseva and Tyutyanov8, Example 1]. However, every group in
![]() $w\mathcal {U}$
has an ordered Sylow tower of supersoluble type [Reference Valisev, Valiseva and Tyutyanov8, Proposition 2.8].
$w\mathcal {U}$
has an ordered Sylow tower of supersoluble type [Reference Valisev, Valiseva and Tyutyanov8, Proposition 2.8].
In [Reference Ballester-Bolinches, Fakieh and Pedraza-Aguilera4], mutually
![]() $sn$
-permutable products in which the factors are w-supersoluble are analysed. The following extension of Theorem 1.2 holds.
$sn$
-permutable products in which the factors are w-supersoluble are analysed. The following extension of Theorem 1.2 holds.
Theorem 1.4 [Reference Ballester-Bolinches, Fakieh and Pedraza-Aguilera4, Theorem 4]
Let
![]() $G = AB$
be the mutually
$G = AB$
be the mutually
![]() $sn$
-permutable product of the subgroups A and B, where A is w-supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is w-supersoluble.
$sn$
-permutable product of the subgroups A and B, where A is w-supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is w-supersoluble.
Assume that
![]() $G = AB$
is the mutually
$G = AB$
is the mutually
![]() $sn$
-permutable product of the subgroups A and B. Then, by [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Proposition 4.1.16 and Corollary 4.1.17],
$sn$
-permutable product of the subgroups A and B. Then, by [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Proposition 4.1.16 and Corollary 4.1.17],
![]() $A \cap B$
is subnormal in G and permutes with every subnormal subgroup of A and B. Assume now that
$A \cap B$
is subnormal in G and permutes with every subnormal subgroup of A and B. Assume now that
![]() $G = AB$
and
$G = AB$
and
![]() $A \cap B$
satisfy this condition. Then G is the mutually
$A \cap B$
satisfy this condition. Then G is the mutually
![]() $sn$
-permutable product of A and B if and only if A permutes with every subnormal subgroup V of B such that
$sn$
-permutable product of A and B if and only if A permutes with every subnormal subgroup V of B such that
![]() $A\cap B\leqslant V $
and B permutes with every subnormal subgroup U of A such that
$A\cap B\leqslant V $
and B permutes with every subnormal subgroup U of A such that
![]() $A\cap B\leqslant U$
. This motivates the following definition.
$A\cap B\leqslant U$
. This motivates the following definition.
Definition 1.5. Let A and B be two subgroups of a group G such that
![]() $G = AB$
. We say that G is the weakly mutually
$G = AB$
. We say that G is the weakly mutually
![]() $sn$
-permutable product of A and B if A permutes with every subnormal subgroup V of B such that
$sn$
-permutable product of A and B if A permutes with every subnormal subgroup V of B such that
![]() $A\cap B\leqslant V $
and B permutes with every subnormal subgroup U of A such that
$A\cap B\leqslant V $
and B permutes with every subnormal subgroup U of A such that
![]() $A\cap B\leqslant U$
.
$A\cap B\leqslant U$
.
Obviously, mutually
![]() $sn$
-permutable products are weakly mutually
$sn$
-permutable products are weakly mutually
![]() $sn$
-permutable, but the converse is not true in general, as the following example shows.
$sn$
-permutable, but the converse is not true in general, as the following example shows.
Example 1.6. Let
![]() $G = \Sigma _{4}$
be the symmetric group of degree
$G = \Sigma _{4}$
be the symmetric group of degree
![]() $4$
. Consider a maximal subgroup A of G which is isomorphic to
$4$
. Consider a maximal subgroup A of G which is isomorphic to
![]() $\Sigma _{3}$
, and
$\Sigma _{3}$
, and
![]() $B = A_4$
, the alternating group of degree
$B = A_4$
, the alternating group of degree
![]() $4$
. Then
$4$
. Then
![]() $G = AB$
is the weakly mutually
$G = AB$
is the weakly mutually
![]() $sn$
-permutable product of the subgroups A and B. However, the product is not mutually
$sn$
-permutable product of the subgroups A and B. However, the product is not mutually
![]() $sn$
-permutable because A does not permute with a subnormal subgroup of order
$sn$
-permutable because A does not permute with a subnormal subgroup of order
![]() $2$
of B.
$2$
of B.
The first goal of this paper to prove weakly mutually
![]() $sn$
-permutable versions of the aforesaid theorems. We show that Theorem 1.4 holds for weakly mutually
$sn$
-permutable versions of the aforesaid theorems. We show that Theorem 1.4 holds for weakly mutually
![]() $sn$
-permutable products.
$sn$
-permutable products.
Theorem A. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the subgroups A and B, where A is w-supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is w-supersoluble.
$sn$
-permutable product of the subgroups A and B, where A is w-supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is w-supersoluble.
The next corollary follows from the proof of Theorem A and generalises Theorem 1.2.
Corollary B. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the subgroups A and B, where A is supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is supersoluble.
$sn$
-permutable product of the subgroups A and B, where A is supersoluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is supersoluble.
The second part of the paper is concerned with weakly mutually
![]() $sn$
-permutable products with nilpotent derived subgroups. Our starting point is the following extension of a classical result of Asaad and Shaalan [Reference Asaad and Shaalan2].
$sn$
-permutable products with nilpotent derived subgroups. Our starting point is the following extension of a classical result of Asaad and Shaalan [Reference Asaad and Shaalan2].
Theorem 1.7 [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1, Theorem C]
Let
![]() $G=AB$
be the mutually
$G=AB$
be the mutually
![]() $sn$
-permutable product of the supersoluble subgroups A and B. If the derived subgroup
$sn$
-permutable product of the supersoluble subgroups A and B. If the derived subgroup
![]() $G'$
of G is nilpotent, then G is supersoluble.
$G'$
of G is nilpotent, then G is supersoluble.
A natural question is whether this result is true for weakly mutually
![]() $sn$
-permutable products under the same conditions. The following example answers this question negatively.
$sn$
-permutable products under the same conditions. The following example answers this question negatively.
Example 1.8. Let
![]() $G=\langle a,b,c :a^5=b^5=c^6=1,ab=ba, a^c=a^2b^3,b^c=a^{-1}b^{-1} \rangle \simeq [C_{5} \times C_{5}]C_{6}$
. Then
$G=\langle a,b,c :a^5=b^5=c^6=1,ab=ba, a^c=a^2b^3,b^c=a^{-1}b^{-1} \rangle \simeq [C_{5} \times C_{5}]C_{6}$
. Then
![]() $G=AB$
is the weakly mutually
$G=AB$
is the weakly mutually
![]() $sn$
-permutable product of
$sn$
-permutable product of
![]() $A=\langle c \rangle $
and
$A=\langle c \rangle $
and
![]() $B=[\langle a \rangle \times \langle b \rangle ]\langle c^3 \rangle $
. Note that B is a normal subgroup of G; therefore, it permutes with every subgroup of A. Moreover,
$B=[\langle a \rangle \times \langle b \rangle ]\langle c^3 \rangle $
. Note that B is a normal subgroup of G; therefore, it permutes with every subgroup of A. Moreover,
![]() $A \cap B=\langle c^3 \rangle $
and the unique subnormal subgroup of B containing
$A \cap B=\langle c^3 \rangle $
and the unique subnormal subgroup of B containing
![]() $A \cap B$
is the whole of B. It is not difficult to see that B is supersoluble. Therefore, A and B are supersoluble and
$A \cap B$
is the whole of B. It is not difficult to see that B is supersoluble. Therefore, A and B are supersoluble and
![]() $G'$
is nilpotent. Moreover, A is nilpotent and B is a normal subgroup of G. Thus, in particular, it permutes with every Sylow subgroup of A.
$G'$
is nilpotent. Moreover, A is nilpotent and B is a normal subgroup of G. Thus, in particular, it permutes with every Sylow subgroup of A.
However, an additional assumption allows us to get supersolubility.
Theorem C. Let
![]() $G=AB$
be the weakly mutually sn-permutable product of the supersoluble subgroups A and B. If B permutes with each Sylow subgroup of A, A permutes with every Sylow subgroup of B and the derived subgroup
$G=AB$
be the weakly mutually sn-permutable product of the supersoluble subgroups A and B. If B permutes with each Sylow subgroup of A, A permutes with every Sylow subgroup of B and the derived subgroup
![]() $G'$
of G is nilpotent, then G is supersoluble.
$G'$
of G is nilpotent, then G is supersoluble.
By [Reference Monakhov7, Theorem 2.6], a group G is w-supersoluble if and only if every metanilpotent subgroup of G is supersoluble. In particular, if we have a group with
![]() $G'$
nilpotent, every w-supersoluble subgroup is supersoluble. Therefore, the following result is clear.
$G'$
nilpotent, every w-supersoluble subgroup is supersoluble. Therefore, the following result is clear.
Corollary D. Let
![]() $G=AB$
be the weakly mutually sn-permutable product of the w-supersoluble subgroups A and B. If B permutes with each Sylow subgroup of A, A permutes with every Sylow subgroup of B and the derived subgroup
$G=AB$
be the weakly mutually sn-permutable product of the w-supersoluble subgroups A and B. If B permutes with each Sylow subgroup of A, A permutes with every Sylow subgroup of B and the derived subgroup
![]() $G'$
of G is nilpotent, then G is w-supersoluble.
$G'$
of G is nilpotent, then G is w-supersoluble.
2 Preliminary results
In this section we will prove some results needed for the proofs of our main results. We start by showing that factor groups of weakly mutually
![]() $sn$
-permutable products are also weakly mutually
$sn$
-permutable products are also weakly mutually
![]() $sn$
-permutable products.
$sn$
-permutable products.
Lemma 2.1. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of A and B, and let
$sn$
-permutable product of A and B, and let
![]() $ N $
be a normal subgroup of
$ N $
be a normal subgroup of
![]() $ G $
. Then
$ G $
. Then
![]() $ G/N=(AN/N)(BN/N) $
is the weakly mutually
$ G/N=(AN/N)(BN/N) $
is the weakly mutually
![]() $sn$
-permutable product of
$sn$
-permutable product of
![]() $AN/N$
and
$AN/N$
and
![]() $BN/N$
.
$BN/N$
.
Proof. Let us consider
![]() $ G/N=(AN/N)(BN/N) $
. Suppose that
$ G/N=(AN/N)(BN/N) $
. Suppose that
![]() $ HN/N $
is a subnormal subgroup of
$ HN/N $
is a subnormal subgroup of
![]() $ AN/N $
such that
$ AN/N $
such that
![]() $ AN/N\cap BN/N\leqslant HN/N $
. Note that
$ AN/N\cap BN/N\leqslant HN/N $
. Note that
![]() $U=HN \cap A$
is a subnormal subgroup of
$U=HN \cap A$
is a subnormal subgroup of
![]() $ A $
such that
$ A $
such that
![]() $UN=HN$
and
$UN=HN$
and
![]() $A \cap B \leq U$
. Since
$A \cap B \leq U$
. Since
![]() $ U $
permutes with
$ U $
permutes with
![]() $ B $
, it follows that
$ B $
, it follows that
![]() $ HN=UN $
permutes with
$ HN=UN $
permutes with
![]() $ BN $
.
$ BN $
.
Interchanging
![]() $ A $
and
$ A $
and
![]() $ B $
and arguing in the same manner proves the result.
$ B $
and arguing in the same manner proves the result.
Lemma 2.2. Let
![]() $ G=AB $
be the weakly mutually
$ G=AB $
be the weakly mutually
![]() $sn$
-permutable product of A and B.
$sn$
-permutable product of A and B.
-
(a) If
 $ H $
is a subnormal subgroup of
$ H $
is a subnormal subgroup of
 $ A $
such that
$ A $
such that
 $ A\cap B \leqslant H $
, then
$ A\cap B \leqslant H $
, then
 $ HB $
is a weakly mutually
$ HB $
is a weakly mutually
 $sn$
-permutable product of H and B.
$sn$
-permutable product of H and B. -
(b) If
 $ A\cap B=1 $
, then
$ A\cap B=1 $
, then
 $ G=AB $
is a totally
$ G=AB $
is a totally
 $sn$
-permutable product of A and B.
$sn$
-permutable product of A and B.
Proof. Since every subnormal subgroup of
![]() $ H $
is a subnormal subgroup of
$ H $
is a subnormal subgroup of
![]() $ A $
, it follows that
$ A $
, it follows that
![]() $ B $
permutes with every subnormal subgroup
$ B $
permutes with every subnormal subgroup
![]() $ L $
of
$ L $
of
![]() $ H $
such that
$ H $
such that
![]() $ A\cap B\leqslant L $
. On the other hand, let
$ A\cap B\leqslant L $
. On the other hand, let
![]() $ M $
be a subnormal subgroup of
$ M $
be a subnormal subgroup of
![]() $ B $
such that
$ B $
such that
![]() $ A\cap B\leqslant M $
. Then we have
$ A\cap B\leqslant M $
. Then we have
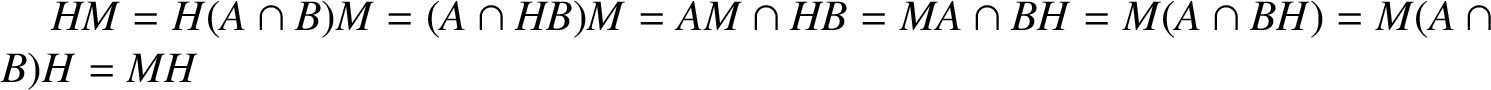 $HM=H(A\cap B)M=(A\cap HB)M=AM\cap HB=MA\cap BH= M(A\cap BH)= M(A\cap B) H=MH $
. Hence
$HM=H(A\cap B)M=(A\cap HB)M=AM\cap HB=MA\cap BH= M(A\cap BH)= M(A\cap B) H=MH $
. Hence
![]() $ HB $
is a weakly mutually
$ HB $
is a weakly mutually
![]() $sn$
-permutable product of H and B.
$sn$
-permutable product of H and B.
For (b), every subnormal subgroup of
![]() $ A $
permutes with
$ A $
permutes with
![]() $ B $
by (a) and every subnormal subgroup of
$ B $
by (a) and every subnormal subgroup of
![]() $ B $
permutes with
$ B $
permutes with
![]() $ A $
. So
$ A $
. So
![]() $ G=AB $
is the mutually
$ G=AB $
is the mutually
![]() $sn$
-permutable product of A and B. Hence
$sn$
-permutable product of A and B. Hence
![]() $ G=AB $
is the totally
$ G=AB $
is the totally
![]() $sn$
-permutable product of A and B since
$sn$
-permutable product of A and B since
![]() $ A\cap B=1 $
.
$ A\cap B=1 $
.
Observe that Lemma 2.2 implies that if
![]() $ G=AB $
is the weakly mutually
$ G=AB $
is the weakly mutually
![]() $ sn $
-permutable product of
$ sn $
-permutable product of
![]() $ A $
and
$ A $
and
![]() $ B $
,
$ B $
,
![]() $ H $
is a subnormal subgroup of
$ H $
is a subnormal subgroup of
![]() $ A $
such that
$ A $
such that
![]() $ A\cap B\leqslant H $
and
$ A\cap B\leqslant H $
and
![]() $ K $
is a subnormal subgroup of
$ K $
is a subnormal subgroup of
![]() $ B $
such that
$ B $
such that
![]() $ A\cap B\leqslant K $
, then
$ A\cap B\leqslant K $
, then
![]() $ HK $
is a weakly mutually
$ HK $
is a weakly mutually
![]() $ sn $
-permutable product of
$ sn $
-permutable product of
![]() $ H $
and
$ H $
and
![]() $ K $
. In the next result we analyse the behaviour of minimal normal subgroups of weakly mutually
$ K $
. In the next result we analyse the behaviour of minimal normal subgroups of weakly mutually
![]() $sn$
-permutable products containing the intersection of the factors.
$sn$
-permutable products containing the intersection of the factors.
Lemma 2.3. Let
![]() $ G=AB $
be the weakly mutually
$ G=AB $
be the weakly mutually
![]() $sn$
-permutable product of A and B. If
$sn$
-permutable product of A and B. If
![]() $ N $
is a minimal normal subgroup of
$ N $
is a minimal normal subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ A\cap B\leqslant N $
, then either
$ A\cap B\leqslant N $
, then either
![]() $ A\cap N=B\cap N=1 $
or
$ A\cap N=B\cap N=1 $
or
![]() $ N=(N\cap A)(N\cap B) $
.
$ N=(N\cap A)(N\cap B) $
.
Proof. Observe that
![]() $ A\cap N $
is a normal subgroup of
$ A\cap N $
is a normal subgroup of
![]() $ A $
such that
$ A $
such that
![]() $ A\cap B\leqslant A\cap N$
and consequently
$ A\cap B\leqslant A\cap N$
and consequently
![]() $ H=(A\cap N)B $
is a subgroup of G. Note that
$ H=(A\cap N)B $
is a subgroup of G. Note that
![]() $ N\cap H = N\cap (A\cap N)B = (A\cap N)(B\cap N)$
. Since
$ N\cap H = N\cap (A\cap N)B = (A\cap N)(B\cap N)$
. Since
![]() $ N\cap H $
is a normal subgroup of
$ N\cap H $
is a normal subgroup of
![]() $ H $
, it follows that
$ H $
, it follows that
![]() $ B $
normalises
$ B $
normalises
![]() $ N\cap H=(A\cap N)(B\cap N) $
.
$ N\cap H=(A\cap N)(B\cap N) $
.
By the same argument,
![]() $ K=A(B\cap N) $
is a subgroup of
$ K=A(B\cap N) $
is a subgroup of
![]() $ G $
such that
$ G $
such that
![]() $ K\cap N= A(B\cap N)\cap N=(A\cap N)(B\cap N) $
. Moreover,
$ K\cap N= A(B\cap N)\cap N=(A\cap N)(B\cap N) $
. Moreover,
![]() $ A $
normalises
$ A $
normalises
![]() $ K\cap N=(A\cap N)(B\cap N) $
. It follows that
$ K\cap N=(A\cap N)(B\cap N) $
. It follows that
![]() $ (A\cap N)(B\cap N) $
is a normal subgroup of
$ (A\cap N)(B\cap N) $
is a normal subgroup of
![]() $ G $
. By the minimality of
$ G $
. By the minimality of
![]() $ N $
,
$ N $
,
![]() $ A\cap N=B\cap N=1 $
or
$ A\cap N=B\cap N=1 $
or
![]() $ N=(N\cap A)(N\cap B) $
as required.
$ N=(N\cap A)(N\cap B) $
as required.
Lemma 2.4. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the subgroups A and B, where B is nilpotent. If B permutes with each Sylow subgroup of A, then
$sn$
-permutable product of the subgroups A and B, where B is nilpotent. If B permutes with each Sylow subgroup of A, then
![]() $ A\cap B $
is a nilpotent subnormal subgroup of
$ A\cap B $
is a nilpotent subnormal subgroup of
![]() $ G $
.
$ G $
.
Proof. It is clear that
![]() $ A\cap B $
is nilpotent. The Sylow subgroups of
$ A\cap B $
is nilpotent. The Sylow subgroups of
![]() $ B $
are normal in
$ B $
are normal in
![]() $ B $
, so
$ B $
, so
![]() $ A\cap B $
permutes with every Sylow subgroup of
$ A\cap B $
permutes with every Sylow subgroup of
![]() $ B $
. Let
$ B $
. Let
![]() $A_{q}$
be a Sylow subgroup of A, with q a prime dividing
$A_{q}$
be a Sylow subgroup of A, with q a prime dividing
![]() $| A |$
. Since
$| A |$
. Since
![]() $ B $
permutes with every Sylow subgroup of
$ B $
permutes with every Sylow subgroup of
![]() $ A $
, it follows that
$ A $
, it follows that
![]() $BA_{q}$
is a subgroup of G. Hence
$BA_{q}$
is a subgroup of G. Hence
![]() $BA_{q} \cap A=A_{q}(A \cap B)$
. Therefore
$BA_{q} \cap A=A_{q}(A \cap B)$
. Therefore
![]() $ A\cap B $
permutes with every Sylow subgroup of
$ A\cap B $
permutes with every Sylow subgroup of
![]() $ A $
. Applying [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Theorem 1.2.14(3)],
$ A $
. Applying [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Theorem 1.2.14(3)],
![]() $ A\cap B $
is a subnormal subgroup of both
$ A\cap B $
is a subnormal subgroup of both
![]() $ A $
and
$ A $
and
![]() $ B $
. By [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Theorem 1.1.7],
$ B $
. By [Reference Ballester-Bolinches, Esteban-Romero and Asaad3, Theorem 1.1.7],
![]() $ A\cap B $
is a subnormal subgroup of
$ A\cap B $
is a subnormal subgroup of
![]() $ G $
.
$ G $
.
Lemma 2.5. Let
![]() $G = AB$
be the weakly mutually
$G = AB$
be the weakly mutually
![]() $sn$
-permutable product of the subgroups A and B, where A is soluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is soluble.
$sn$
-permutable product of the subgroups A and B, where A is soluble and B is nilpotent. If B permutes with each Sylow subgroup of A, then the group G is soluble.
Proof. Suppose that the theorem is false, and let
![]() $ G $
be a minimal counterexample. If
$ G $
be a minimal counterexample. If
![]() $ N $
is a minimal normal subgroup of
$ N $
is a minimal normal subgroup of
![]() $ G $
, then
$ G $
, then
![]() $ G/N=(AN/N)(BN/N) $
is the weakly mutually
$ G/N=(AN/N)(BN/N) $
is the weakly mutually
![]() $sn$
-permutable product of the subgroups
$sn$
-permutable product of the subgroups
![]() $AN/N$
and
$AN/N$
and
![]() $BN/N$
by Lemma 2.1. Since
$BN/N$
by Lemma 2.1. Since
![]() $BN/N$
permutes with each Sylow subgroup of
$BN/N$
permutes with each Sylow subgroup of
![]() $AN/N$
, it follows that
$AN/N$
, it follows that
![]() $ G/N $
is soluble by the minimality of G. Let
$ G/N $
is soluble by the minimality of G. Let
![]() $ N_{1} $
and
$ N_{1} $
and
![]() $ N_{2} $
be two minimal subgroups of
$ N_{2} $
be two minimal subgroups of
![]() $ G $
. Then
$ G $
. Then
![]() $ G\cong G/(N_{1}\cap N_{2}) $
is soluble, a contradiction. Hence
$ G\cong G/(N_{1}\cap N_{2}) $
is soluble, a contradiction. Hence
![]() $ G $
has a unique minimal normal subgroup
$ G $
has a unique minimal normal subgroup
![]() $ N $
of
$ N $
of
![]() $ G $
and we may assume that
$ G $
and we may assume that
![]() $ N $
is nonabelian. This means that
$ N $
is nonabelian. This means that
![]() $ \textbf {F}(G)=1 $
.
$ \textbf {F}(G)=1 $
.
On the other hand,
![]() $ A\cap B \leqslant \textbf {F}(G) $
using Lemma 2.4. Therefore
$ A\cap B \leqslant \textbf {F}(G) $
using Lemma 2.4. Therefore
![]() $ A\cap B=1 $
and then
$ A\cap B=1 $
and then
![]() $ G=AB $
is the totally
$ G=AB $
is the totally
![]() $sn$
-permutable product of
$sn$
-permutable product of
![]() $ A $
and
$ A $
and
![]() $ B $
. The result then follows by applying [Reference Carocca5, Theorem 6].
$ B $
. The result then follows by applying [Reference Carocca5, Theorem 6].
Lemma 2.6 [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1, Lemma 3]
Let
![]() $ G $
be a primitive group and let
$ G $
be a primitive group and let
![]() $ N $
be its unique minimal normal subgroup. Assume that
$ N $
be its unique minimal normal subgroup. Assume that
![]() $ G/N $
is supersoluble. If
$ G/N $
is supersoluble. If
![]() $ N $
is a
$ N $
is a
![]() $ p $
-group, where
$ p $
-group, where
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ |G| $
, then
$ |G| $
, then
![]() $ N=\mathbf {F}(G)=\mathbf {O}_{p}(G) $
is a Sylow
$ N=\mathbf {F}(G)=\mathbf {O}_{p}(G) $
is a Sylow
![]() $ p $
-subgroup of G.
$ p $
-subgroup of G.
3 Main results
We are ready to prove our main results.
Proof of Theorem A
Suppose the theorem is not true and let
![]() $ G $
be a minimal counterexample. We shall prove our theorem in five steps.
$ G $
be a minimal counterexample. We shall prove our theorem in five steps.
(a)
![]() $ G $
is a primitive soluble group with a unique minimal normal subgroup
$ G $
is a primitive soluble group with a unique minimal normal subgroup
![]() $ N $
and
$ N $
and
![]() $ N=\textbf {C}_{G}(N)=\textbf {F}(G)=\textbf {O}_{p}(G) $
for a prime
$ N=\textbf {C}_{G}(N)=\textbf {F}(G)=\textbf {O}_{p}(G) $
for a prime
![]() $ p $
. Let
$ p $
. Let
![]() $ N $
be a minimal normal subgroup of
$ N $
be a minimal normal subgroup of
![]() $ G $
. By Lemma 2.1,
$ G $
. By Lemma 2.1,
![]() $ G/N=(AN/N)(BN/N) $
is a weakly mutually
$ G/N=(AN/N)(BN/N) $
is a weakly mutually
![]() $ sn $
-permutable product of
$ sn $
-permutable product of
![]() $ AN/N $
and
$ AN/N $
and
![]() $ BN/N $
and it is clear that
$ BN/N $
and it is clear that
![]() $ BN/N $
permutes with every Sylow subgroup of
$ BN/N $
permutes with every Sylow subgroup of
![]() $ AN/N $
. Moreover,
$ AN/N $
. Moreover,
![]() $ AN/N $
is
$ AN/N $
is
![]() $ w $
-supersoluble and
$ w $
-supersoluble and
![]() $ BN/N $
is nilpotent. By the minimality of
$ BN/N $
is nilpotent. By the minimality of
![]() $ G $
, it follows that
$ G $
, it follows that
![]() $ G/N $
is
$ G/N $
is
![]() $ w $
-supersoluble. Note that
$ w $
-supersoluble. Note that
![]() $ w\mathcal {U} $
, the class of finite
$ w\mathcal {U} $
, the class of finite
![]() $ w $
-supersoluble groups, is a saturated formation of soluble groups by [Reference Valisev, Valiseva and Tyutyanov8, Theorems 2.3 and 2.7]. This implies that
$ w $
-supersoluble groups, is a saturated formation of soluble groups by [Reference Valisev, Valiseva and Tyutyanov8, Theorems 2.3 and 2.7]. This implies that
![]() $ G $
is a primitive soluble group and so
$ G $
is a primitive soluble group and so
![]() $ G $
has a unique minimal normal subgroup
$ G $
has a unique minimal normal subgroup
![]() $ N $
with
$ N $
with
![]() $ N=\textbf {C}_{G}(N)=\textbf {F}(G)=\textbf {O}_{p}(G) $
for some prime
$ N=\textbf {C}_{G}(N)=\textbf {F}(G)=\textbf {O}_{p}(G) $
for some prime
![]() $ p $
as required.
$ p $
as required.
(b) The subgroup
![]() $ BN $
is
$ BN $
is
![]() $ w $
-supersoluble and
$ w $
-supersoluble and
![]() $ 1\not = A\cap B\leqslant N $
. If
$ 1\not = A\cap B\leqslant N $
. If
![]() $ A\cap B=1 $
, then the result follows by Lemma 2.2 and Theorem 1.4. Applying Lemma 2.4, it follows that
$ A\cap B=1 $
, then the result follows by Lemma 2.2 and Theorem 1.4. Applying Lemma 2.4, it follows that
![]() $ A\cap B $
is a nilpotent subnormal subgroup of
$ A\cap B $
is a nilpotent subnormal subgroup of
![]() $ G $
. Therefore
$ G $
. Therefore
![]() $ 1\not = A\cap B \leqslant \textbf {F}(G)=N $
and so
$ 1\not = A\cap B \leqslant \textbf {F}(G)=N $
and so
![]() $ N= (N\cap A)(N\cap B) $
by Lemma 2.3. Hence
$ N= (N\cap A)(N\cap B) $
by Lemma 2.3. Hence
![]() $ NB=(N\cap A)(N\cap B)B=(N\cap A)B $
is a weakly mutually
$ NB=(N\cap A)(N\cap B)B=(N\cap A)B $
is a weakly mutually
![]() $ sn $
-permutable product of
$ sn $
-permutable product of
![]() $ N\cap A $
and
$ N\cap A $
and
![]() $ B $
. Also note that
$ B $
. Also note that
![]() $ B $
permutes with every Sylow subgroup of
$ B $
permutes with every Sylow subgroup of
![]() $ N\cap A $
(there is only one Sylow subgroup of
$ N\cap A $
(there is only one Sylow subgroup of
![]() $ N\cap A $
, which is
$ N\cap A $
, which is
![]() $ N\cap A $
). If
$ N\cap A $
). If
![]() $ NB < G $
, then
$ NB < G $
, then
![]() $ NB $
is
$ NB $
is
![]() $ w $
-supersoluble by the choice of
$ w $
-supersoluble by the choice of
![]() $ G $
. So we may assume that
$ G $
. So we may assume that
![]() $ G=NB $
. In this case, consider a subgroup
$ G=NB $
. In this case, consider a subgroup
![]() $ N_{1} \leqslant A\cap B\leqslant N $
. Note that
$ N_{1} \leqslant A\cap B\leqslant N $
. Note that
![]() $ N_{1} $
is normal in
$ N_{1} $
is normal in
![]() $ N $
since
$ N $
since
![]() $ N $
is abelian. Hence
$ N $
is abelian. Hence
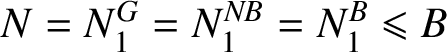 $ N=N_{1}^{G}=N_{1}^{NB}=N_{1}^{B}\leqslant B $
and
$ N=N_{1}^{G}=N_{1}^{NB}=N_{1}^{B}\leqslant B $
and
![]() $ G=B $
, a contradiction. Hence the result follows.
$ G=B $
, a contradiction. Hence the result follows.
(c)
![]() $ N $
is the Sylow
$ N $
is the Sylow
![]() $ p\!$
-subgroup of G and
$ p\!$
-subgroup of G and
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ |G| $
. Let
$ |G| $
. Let
![]() $ q $
be the largest prime dividing
$ q $
be the largest prime dividing
![]() $ |G| $
and suppose that
$ |G| $
and suppose that
![]() $ q\not = p $
. Suppose first that
$ q\not = p $
. Suppose first that
![]() $ q $
divides
$ q $
divides
![]() $ |BN| $
. Since
$ |BN| $
. Since
![]() $ BN $
has a Sylow tower of supersoluble type,
$ BN $
has a Sylow tower of supersoluble type,
![]() $ BN $
has a unique Sylow
$ BN $
has a unique Sylow
![]() $ q $
-subgroup, say
$ q $
-subgroup, say
![]() $ (BN)_{q} $
. This means that
$ (BN)_{q} $
. This means that
![]() $ (BN)_{q} $
centralises
$ (BN)_{q} $
centralises
![]() $ N $
. Thus
$ N $
. Thus
![]() $ (BN)_{q}=1 $
, since
$ (BN)_{q}=1 $
, since
![]() $ \mathbf {C}_{G}(N)=N $
, a contradiction.
$ \mathbf {C}_{G}(N)=N $
, a contradiction.
We may assume that
![]() $ q $
divides
$ q $
divides
![]() $ |A| $
but does not divide
$ |A| $
but does not divide
![]() $ |BN| $
. Since
$ |BN| $
. Since
![]() $ A $
has a Sylow tower of supersoluble type,
$ A $
has a Sylow tower of supersoluble type,
![]() $ A $
has a unique Sylow
$ A $
has a unique Sylow
![]() $ q $
-subgroup,
$ q $
-subgroup,
![]() $ A_{q} $
say. This means that
$ A_{q} $
say. This means that
![]() $ A_{q} $
is normalised by
$ A_{q} $
is normalised by
![]() $ N\cap A $
. Consider
$ N\cap A $
. Consider
![]() $ A_{q}(N\cap B)=A_{q}(A\cap B)(N\cap B) $
, a weakly mutually permutable product of
$ A_{q}(N\cap B)=A_{q}(A\cap B)(N\cap B) $
, a weakly mutually permutable product of
![]() $ A_{q}(A\cap B) $
and
$ A_{q}(A\cap B) $
and
![]() $ N\cap B $
by Lemma 2.2. Also
$ N\cap B $
by Lemma 2.2. Also
![]() $ N\cap B $
permutes with each Sylow subgroup of
$ N\cap B $
permutes with each Sylow subgroup of
![]() $ A_{q}(A\cap B) $
. Suppose that
$ A_{q}(A\cap B) $
. Suppose that
![]() $ A_{q}(N\cap B) < G $
. Then
$ A_{q}(N\cap B) < G $
. Then
![]() $ A_{q}(N\cap B) $
is
$ A_{q}(N\cap B) $
is
![]() $ w $
-supersoluble by the choice of
$ w $
-supersoluble by the choice of
![]() $ G $
. It follows that
$ G $
. It follows that
![]() $ A_{q}(N\cap B) $
has a unique Sylow
$ A_{q}(N\cap B) $
has a unique Sylow
![]() $ q $
-subgroup since it has a Sylow tower of supersoluble type. In other words,
$ q $
-subgroup since it has a Sylow tower of supersoluble type. In other words,
![]() $ A_{q} $
is normalised by
$ A_{q} $
is normalised by
![]() $ N\cap B $
. Hence
$ N\cap B $
. Hence
![]() $ A_{q} $
is normalised by
$ A_{q} $
is normalised by
![]() $ (N\cap A)(N\cap B)=N $
. This means that
$ (N\cap A)(N\cap B)=N $
. This means that
![]() $ A_{q} $
centralises
$ A_{q} $
centralises
![]() $ N $
, a contradiction. We may assume that
$ N $
, a contradiction. We may assume that
![]() $ A_{q}(N\cap B)=G $
. Then
$ A_{q}(N\cap B)=G $
. Then
![]() $ N \cap B=B $
and so
$ N \cap B=B $
and so
![]() $ B $
is an elementary abelian
$ B $
is an elementary abelian
![]() $ p $
-group. Moreover,
$ p $
-group. Moreover,
![]() $ A=A_{q}(A\cap B) $
. Since
$ A=A_{q}(A\cap B) $
. Since
![]() $ A\cap B $
is a Sylow
$ A\cap B $
is a Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ A $
which is subnormal in
$ A $
which is subnormal in
![]() $ A $
, it is normal in
$ A $
, it is normal in
![]() $ A $
. Hence
$ A $
. Hence
![]() $ A\cap B $
is normal in
$ A\cap B $
is normal in
![]() $ G $
because
$ G $
because
![]() $ A\cap B $
is normal in the abelian group
$ A\cap B $
is normal in the abelian group
![]() $ B $
. By the minimality of
$ B $
. By the minimality of
![]() $ N $
, it follows that
$ N $
, it follows that
![]() $ N=A\cap B $
, that is,
$ N=A\cap B $
, that is,
![]() $ G=A_{q}(N\cap B)=A_{q}(A \cap B)=A $
, a contradiction. Therefore
$ G=A_{q}(N\cap B)=A_{q}(A \cap B)=A $
, a contradiction. Therefore
![]() $ p $
is the largest prime dividing
$ p $
is the largest prime dividing
![]() $ |G| $
.
$ |G| $
.
We now prove that
![]() $ N $
is the Sylow
$ N $
is the Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ G $
. Since
$ G $
. Since
![]() $ G $
is a primitive soluble group,
$ G $
is a primitive soluble group,
![]() $ G=NM $
, where
$ G=NM $
, where
![]() $ M $
is a maximal subgroup of
$ M $
is a maximal subgroup of
![]() $ G $
and
$ G $
and
![]() $ N\cap M=1 $
. Then
$ N\cap M=1 $
. Then
![]() $ M\cong G/N $
is
$ M\cong G/N $
is
![]() $ w $
-supersoluble. By [Reference Doerk and Hawkes6, Theorem A.15.6],
$ w $
-supersoluble. By [Reference Doerk and Hawkes6, Theorem A.15.6],
![]() $ \textbf {O}_{p}(M)=1 $
. If
$ \textbf {O}_{p}(M)=1 $
. If
![]() $ p $
divides
$ p $
divides
![]() $ |M| $
, then since
$ |M| $
, then since
![]() $ M $
has a Sylow tower of supersoluble type,
$ M $
has a Sylow tower of supersoluble type,
![]() $ \textbf {O}_{p}(M)\not =1 $
, a contradiction. Hence
$ \textbf {O}_{p}(M)\not =1 $
, a contradiction. Hence
![]() $ p $
does not divide
$ p $
does not divide
![]() $ |M| $
and therefore
$ |M| $
and therefore
![]() $ N $
is the unique Sylow
$ N $
is the unique Sylow
![]() $ p $
-subgroup of
$ p $
-subgroup of
![]() $ G $
.
$ G $
.
(d)
![]() $ N $
is contained in
$ N $
is contained in
![]() $ A $
and
$ A $
and
![]() $ N $
is not contained in
$ N $
is not contained in
![]() $ B $
. Suppose that
$ B $
. Suppose that
![]() $ B $
is a
$ B $
is a
![]() $ p $
-group. Then
$ p $
-group. Then
![]() $ G=AN $
. Let
$ G=AN $
. Let
![]() $ N_{1}\leqslant A\cap B $
. Since
$ N_{1}\leqslant A\cap B $
. Since
![]() $ B $
is abelian,
$ B $
is abelian,
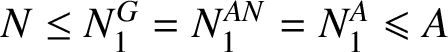 $ N \leq N_{1}^{G}=N_{1}^{AN}=N_{1}^{A}\leqslant A $
and so
$ N \leq N_{1}^{G}=N_{1}^{AN}=N_{1}^{A}\leqslant A $
and so
![]() $ G=AN=A $
, a contradiction. So we may assume that
$ G=AN=A $
, a contradiction. So we may assume that
![]() $ B $
is not a
$ B $
is not a
![]() $ p $
-group. If
$ p $
-group. If
![]() $ N $
is contained in
$ N $
is contained in
![]() $ B $
, then since
$ B $
, then since
![]() $ B $
is nilpotent and
$ B $
is nilpotent and
![]() $ N =\textbf {C}_{G}(N)$
, it follows that
$ N =\textbf {C}_{G}(N)$
, it follows that
![]() $ B $
is a
$ B $
is a
![]() $ p $
-group, a contradiction. Therefore
$ p $
-group, a contradiction. Therefore
![]() $ N $
is not contained in
$ N $
is not contained in
![]() $ B $
. Hence
$ B $
. Hence
![]() $ B $
has a nontrivial Hall
$ B $
has a nontrivial Hall
![]() $ p' $
-subgroup,
$ p' $
-subgroup,
![]() $ B_{p'} $
, which is normal in
$ B_{p'} $
, which is normal in
![]() $ B $
. Consequently,
$ B $
. Consequently,
![]() $ AB_{p'}=A(A\cap B)B_{p'} $
is a subgroup of G. Then
$ AB_{p'}=A(A\cap B)B_{p'} $
is a subgroup of G. Then
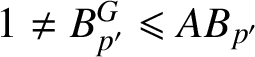 $ 1\not = B_{p'}^{G}\leqslant AB_{p'} $
and so
$ 1\not = B_{p'}^{G}\leqslant AB_{p'} $
and so
![]() $ N \leqslant AB_{p'}$
. Hence
$ N \leqslant AB_{p'}$
. Hence
![]() $ N\leqslant A $
as required.
$ N\leqslant A $
as required.
(e) Final contradiction. Let
![]() $ A_{p'} $
be a Hall
$ A_{p'} $
be a Hall
![]() $ p' $
-subgroup of
$ p' $
-subgroup of
![]() $ A $
. If
$ A $
. If
![]() $ A_{p'}=1 $
, then
$ A_{p'}=1 $
, then
![]() $ G=BN $
is
$ G=BN $
is
![]() $ w $
-supersoluble by (b), a contradiction. Hence
$ w $
-supersoluble by (b), a contradiction. Hence
![]() $ A_{p'}\not = 1 $
. Since
$ A_{p'}\not = 1 $
. Since
![]() $ B $
permutes with every Sylow subgroup of
$ B $
permutes with every Sylow subgroup of
![]() $ A $
, it follows that
$ A $
, it follows that
![]() $ A_{p'}B $
is a subgroup of
$ A_{p'}B $
is a subgroup of
![]() $ G $
. But
$ G $
. But
![]() $ N $
is not contained in
$ N $
is not contained in
![]() $ B $
, so
$ B $
, so
![]() $ A_{p'}B $
is a proper subgroup of
$ A_{p'}B $
is a proper subgroup of
![]() $ G $
. Since
$ G $
. Since
![]() $ NA_{p'}B=G $
, it follows that
$ NA_{p'}B=G $
, it follows that
![]() $ N\cap A_{p'}B=N\cap B $
is normal in
$ N\cap A_{p'}B=N\cap B $
is normal in
![]() $ G $
. The minimality of
$ G $
. The minimality of
![]() $ N $
implies that
$ N $
implies that
![]() $ N=N\cap B $
or
$ N=N\cap B $
or
![]() $ N\cap B=1 $
. If
$ N\cap B=1 $
. If
![]() $ N=N\cap B $
, we get a contradiction with (d). Therefore
$ N=N\cap B $
, we get a contradiction with (d). Therefore
![]() $ N\cap B=1 $
, and then
$ N\cap B=1 $
, and then
![]() $ A\cap B\leqslant N\cap B=1 $
, contradicting (b).
$ A\cap B\leqslant N\cap B=1 $
, contradicting (b).
Proof of Theorem C
Assume the result is not true and let G be a minimal counterexample. It is clear that
![]() $G' \neq 1$
, A and B are proper subgroups of G, and G is a primitive soluble group. Hence there exists a unique minimal normal subgroup N of G, such that
$G' \neq 1$
, A and B are proper subgroups of G, and G is a primitive soluble group. Hence there exists a unique minimal normal subgroup N of G, such that
![]() $N=F(G)=C_{G}(N)$
. Moreover,
$N=F(G)=C_{G}(N)$
. Moreover,
![]() $G'=N$
. We may assume that
$G'=N$
. We may assume that
![]() $A' \neq 1$
and
$A' \neq 1$
and
![]() $B' \neq 1$
, otherwise A or B is nilpotent and the result follows from Corollary B. If
$B' \neq 1$
, otherwise A or B is nilpotent and the result follows from Corollary B. If
![]() $A \cap B=1$
, then G is the mutually
$A \cap B=1$
, then G is the mutually
![]() $sn$
-permutable product of A and B. By [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1, Theorem C], the group is supersoluble, a contradiction. Thus we may assume
$sn$
-permutable product of A and B. By [Reference Alejandre, Ballester-Bolinches, Cossey and Pedraza-Aguilera1, Theorem C], the group is supersoluble, a contradiction. Thus we may assume
![]() $A \cap B \neq 1$
. Since A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, it follows that
$A \cap B \neq 1$
. Since A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, it follows that
![]() $A \cap B$
permutes with every Sylow subgroup of A and every Sylow subgroup of B. Hence
$A \cap B$
permutes with every Sylow subgroup of A and every Sylow subgroup of B. Hence
![]() $A \cap B$
is subnormal in A and it is a subnormal subgroup of B. Let
$A \cap B$
is subnormal in A and it is a subnormal subgroup of B. Let
![]() $N_{1}$
denote a minimal normal subgroup of A such that
$N_{1}$
denote a minimal normal subgroup of A such that
![]() $N_{1} \leq A'$
. Since A is supersoluble, it is clear that
$N_{1} \leq A'$
. Since A is supersoluble, it is clear that
![]() $| N_{1} | =p$
. Note that
$| N_{1} | =p$
. Note that
![]() $N_{1}(A \cap B)$
is a subnormal subgroup of A. Therefore
$N_{1}(A \cap B)$
is a subnormal subgroup of A. Therefore
![]() $BN_{1}(A \cap B)=BN_{1}$
is a subgroup of G. Now
$BN_{1}(A \cap B)=BN_{1}$
is a subgroup of G. Now
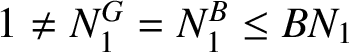 $1 \neq N_{1}^G=N_{1}^B \leq BN_{1}$
. Hence
$1 \neq N_{1}^G=N_{1}^B \leq BN_{1}$
. Hence
![]() $N \leq BN_{1}$
and then
$N \leq BN_{1}$
and then
![]() $N=N_{1}(N \cap B)$
. Consequently, either
$N=N_{1}(N \cap B)$
. Consequently, either
![]() $N_{1} \leq N \cap B$
or
$N_{1} \leq N \cap B$
or
![]() $N_{1} \leq N \cap B$
. Denote
$N_{1} \leq N \cap B$
. Denote
![]() $T=BN$
. If
$T=BN$
. If
![]() $N_{1} \leq N \cap B$
, then
$N_{1} \leq N \cap B$
, then
![]() $T=B$
is a supersoluble normal subgroup of G. Assume
$T=B$
is a supersoluble normal subgroup of G. Assume
![]() $N_{1} \cap (N \cap B)=1$
. Then
$N_{1} \cap (N \cap B)=1$
. Then
![]() $N \cap B$
is a maximal subgroup of N and so T is the weakly mutually
$N \cap B$
is a maximal subgroup of N and so T is the weakly mutually
![]() $sn$
-permutable product of B and N. Consequently, T satisfies the hypotheses of the theorem. If T is a proper subgroup of G, then
$sn$
-permutable product of B and N. Consequently, T satisfies the hypotheses of the theorem. If T is a proper subgroup of G, then
![]() $T=BN$
is supersoluble. Assume that
$T=BN$
is supersoluble. Assume that
![]() $G = BN$
. Then B is a maximal subgroup of G such that
$G = BN$
. Then B is a maximal subgroup of G such that
![]() $B \cap N = 1$
,
$B \cap N = 1$
,
![]() $B' \leq N \cap B=1$
and B is nilpotent. By Corollary B, G is supersoluble, contrary to assumption. Hence either B is a normal subgroup of G or
$B' \leq N \cap B=1$
and B is nilpotent. By Corollary B, G is supersoluble, contrary to assumption. Hence either B is a normal subgroup of G or
![]() $BN$
is a supersoluble normal subgroup of G.
$BN$
is a supersoluble normal subgroup of G.
Arguing in an analogous manner with A shows that if
![]() $AN$
is a proper subgroup of G, then it is supersoluble. Consequently if
$AN$
is a proper subgroup of G, then it is supersoluble. Consequently if
![]() $BN$
and
$BN$
and
![]() $AN$
are both proper subgroups of G, then G is the product of two supersoluble normal subgroups with
$AN$
are both proper subgroups of G, then G is the product of two supersoluble normal subgroups with
![]() $G'$
nilpotent. Then G is supersoluble, a contradiction. Therefore we may assume that
$G'$
nilpotent. Then G is supersoluble, a contradiction. Therefore we may assume that
![]() $G=BN$
or
$G=BN$
or
![]() $G=AN$
. Suppose without loss of generality that
$G=AN$
. Suppose without loss of generality that
![]() $G=BN$
. Then
$G=BN$
. Then
![]() $N \cap B$
is a normal subgroup of G. If
$N \cap B$
is a normal subgroup of G. If
![]() $N \cap B=N$
, then
$N \cap B=N$
, then
![]() $G=B$
, a contradiction. Hence
$G=B$
, a contradiction. Hence
![]() $N \cap B=1$
. Now
$N \cap B=1$
. Now
![]() $B' \leq N \cap B=1$
and B is nilpotent, the final contradiction.
$B' \leq N \cap B=1$
and B is nilpotent, the final contradiction.