14 results
Minimal monoids generating varieties with complex subvariety lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 617-642
-
- Article
-
- You have access
- HTML
- Export citation
On semidirectly closed pseudovarieties of finite semigroups and monoids
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 612-627
- Print publication:
- September 2022
-
- Article
- Export citation
On semidirectly closed non-aperiodic pseudovarieties of finite monoids
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 24 August 2020, pp. 913-928
-
- Article
- Export citation
Merge Decompositions, Two-sided Krohn–Rhodes, and Aperiodic Pointlikes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 199-208
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
ON FREE SPECTRA OF LOCALLY TESTABLE SEMIGROUP VARIETIES
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 10 March 2011, pp. 623-629
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
VARIETIES GENERATED BY COMPLETELY 0-SIMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 375-403
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
NORMALLY ORDERED SEMIGROUPS
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 2 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 325-333
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Polyhedral convex cones and the equational theory of the bicyclic semigroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 63-96
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Rees matrix semigroups and the regular semidirect product
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-60
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Some Semigroup Laws in Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 1 / 01 March 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-96
- Print publication:
- 01 March 2001
-
- Article
-
- You have access
- Export citation
Associativity of the regular semidirect product of existence varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-115
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
On existence varieties of orthodox semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-125
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
On the Lattice of Existence Varieties of Locally Inverse Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-20
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
An Order-Theoretical Characterization of Varieties of Bands
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 3 / 01 September 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 368-374
- Print publication:
- 01 September 1991
-
- Article
-
- You have access
- Export citation

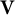
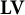
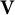
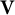
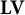
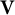
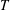
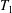
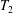
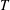
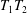
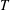
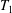
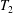
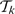
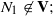 (iii)
(iii) 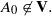 The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.
The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.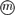
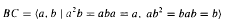 or in the semigroup
or in the semigroup 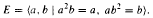 . The semigroups
. The semigroups 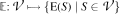 which assigns to each existence variety
which assigns to each existence variety 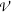 of locally inverse semigroups the class of all pseudosemilattices of idempotents of members of
of locally inverse semigroups the class of all pseudosemilattices of idempotents of members of 