Profinite algebras are exactly those that are isomorphic to inverse limits of finite algebras. Such algebras are naturally equipped with Boolean topologies. A variety ${\cal V}$ is standard if every Boolean topological algebra with the algebraic reduct in ${\cal V}$ is profinite.

We show that there is no algorithm which takes as input a finite algebra A of a finite type and decide whether the variety $V\left( {\bf{A}} \right)$ generated by A is standard. We also show the undecidability of some related properties. In particular, we solve a problem posed by Clark, Davey, Freese, and Jackson.

We accomplish this by combining two results. The first one is Moore’s theorem saying that there is no algorithm which takes as input a finite algebra A of a finite type and decides whether $V\left( {\bf{A}} \right)$ has definable principal subcongruences. The second is our result saying that possessing definable principal subcongruences yields possessing finitely determined syntactic congruences for varieties. The latter property is known to yield standardness.

Let 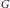$G$ be an infinite discrete group and let 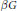$\beta G$ be the Stone-Čech compactification of 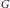$G$. We take the points of 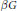$\beta G$ to be the ultrafilters on 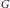$G$, identifying the principal ultrafilters with the points of 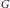$G$. The set 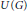$U\left( G \right)$ of uniform ultrafilters on 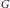$G$ is a closed two-sided ideal of 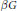$\beta G$. For every 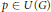$p\,\in \,U\left( G \right)$, define 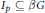${{I}_{p}}\,\subseteq \,\beta G$ by 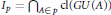${{I}_{p}}\,=\,{{\bigcap }_{A\in p}}\text{cl}\left( GU\left( A \right) \right)$, where 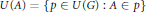$U\left( A \right)\,=\,\left\{ p\,\in \,U\left( G \right)\,:\,A\in \,p \right\}$. We show that if 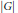$\left| G \right|$ is a regular cardinal, then 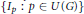$\left\{ {{I}_{p}}\,:\,p\,\in \,U\left( G \right) \right\}$ is the finest decomposition of 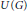$U\left( G \right)$ into closed left ideals of 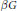$\beta G$ such that the corresponding quotient space of 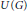$U\left( G \right)$ is Hausdorff.

We present a structure theorem for a broad class of homeomorphisms of finite order on countable zero dimensional spaces. As applications we show the following.

1. (a) Every countable nondiscrete topological group not containing an open Boolean subgroup can be partitioned into infinitely many dense subsets.

2. (b) If $G$ is a countably infinite Abelian group with finitely many elements of order 2 and $\beta G$ is the Stone–Čech compactification of $G$ as a discrete semigroup, then for every idempotent $p\,\,\in \,\,\beta G\backslash \{0\}$, the subset $\{p,-p\}\subset \beta G$ generates algebraically the free product of one-element semigroups $\{p\}$ and $\{-p\}$.

We consider minimal left ideals L of the universal semigroup compactification of a topological semigroup S. We show that the enveloping semigroup of L is homeomorphically isomorphic to if and only if given q ≠ r in , there is some p in the smallest ideal of with qp ≠ rp. We derive several conditions, some involving minimal flows, which are equivalent to the ability to separate q and r in this fashion, and then specialize to the case that S = , and the compactification is . Included is the statement that some set A whose characteristic function is uniformly recurrent has .