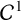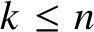6 results
REGULARITY OF AML FUNCTIONS IN TWO-DIMENSIONAL NORMED SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 406-430
- Print publication:
- June 2023
-
- Article
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
On the Construction of Hölder and Proximal Subderivatives
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 4 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-507
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation
Intégration Du Sous-Différentiel Proximal: Un Contre Exemple
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 2 / 01 April 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 242-265
- Print publication:
- 01 April 1998
-
- Article
-
- You have access
- Export citation
Mean Oscillation and Besov Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 4 / 01 December 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 474-480
- Print publication:
- 01 December 1985
-
- Article
-
- You have access
- Export citation