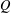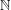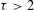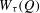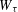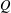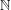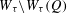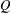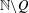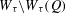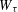4 results
HAUSDORFF DIMENSIONS OF SOME LIMINF SETS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 101-120
- Print publication:
- January 2015
-
- Article
- Export citation
Hausdorff dimensions of self-similar and self-affine fractals in the Heisenberg group
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 1 / July 2005
- Published online by Cambridge University Press:
- 22 June 2005, pp. 153-183
- Print publication:
- July 2005
-
- Article
- Export citation
HESSIAN MEASURES OF CONVEX FUNCTIONS AND APPLICATIONS TO AREA MEASURES
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 04 February 2005, pp. 221-235
- Print publication:
- February 2005
-
- Article
- Export citation
SMOOTHNESS OF THE $L^{\lowercase{q}}$-SPECTRUM OF SELF-SIMILAR MEASURES WITH OVERLAPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 68 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 08 August 2003, pp. 102-118
- Print publication:
- August 2003
-
- Article
- Export citation