A magma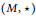$\left( M,\star \right)$ is a nonempty set with a binary operation. A double magma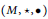$\left( M,\star ,\bullet \right)$ is a nonempty set with two binary operations satisfying the interchange law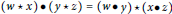$\left( w\star x \right)\bullet \left( y\star z \right)=\left( w\bullet y \right)\star \left( x\bullet z \right)$. We call a double magma proper if the two operations are distinct, and commutative if the operations are commutative. A double semigroup, first introduced by Kock, is a double magma for which both operations are associative. Given a non-trivial group 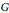$G$ we define a system of two magma 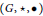$\left( G,\star ,\bullet \right)$ using the commutator operations 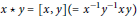$x\star y=\left[ x,y \right]\left( ={{x}^{-1}}{{y}^{-1}}xy \right)$ and 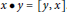$x\bullet y=\left[ y,x \right]$. We show that 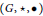$\left( G,\star ,\bullet \right)$ is a double magma if and only if 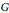$G$ satisfies the commutator laws 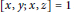$\left[ x,y;x,z \right]=1$ and 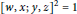${{\left[ w,x;y,z \right]}^{2}}=1$. We note that the first law defines the class of 3-metabelian groups. If both these laws hold in 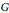$G$, the double magma is proper if and only if there exist 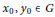${{x}_{0}},{{y}_{0}}\in G$ for which ${{\left[ {{x}_{0}},{{y}_{0}} \right]}^{2}}\ne 1$. This double magma is a double semigroup if and only if 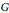$G$ is nilpotent of class two. We construct a specific example of a proper double semigroup based on the dihedral group of order 16. In addition, we comment on a similar construction for rings using Lie commutators.