7 results
Continued Fraction Analysis of the Duration of an Excursion in an M/M/∞ System
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 165-183
- Print publication:
- March 1998
-
- Article
- Export citation
Transient characteristics of an M/M/∞ system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 862-888
- Print publication:
- September 1995
-
- Article
- Export citation
A Class of Generalized Hypergeometric Functions in Several Variables
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 6 / 01 December 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1317-1338
- Print publication:
- 01 December 1992
-
- Article
-
- You have access
- Export citation
Complex Weight Functions for Classical Orthogonal Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 6 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1294-1308
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation
Some Continued Fractions of Ramanujan and Meixner-Pollaczek Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 2 / 01 June 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 177-181
- Print publication:
- 01 June 1989
-
- Article
-
- You have access
- Export citation
Convergence and Analytic Continuation for a Class of Regular C-Fractions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 4 / 01 December 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 411-421
- Print publication:
- 01 December 1985
-
- Article
-
- You have access
- Export citation
Orthogonal Polynomials With Weight Function (1 - x)α( l + x)β + Mδ(x + 1) + Nδ(x - 1)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 2 / 01 June 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 205-214
- Print publication:
- 01 June 1984
-
- Article
-
- You have access
- Export citation

 for an even larger class of
for an even larger class of 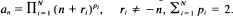 .
.