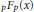6 results
A Generalised Kummer-Type Transformation for the pFp(x) Hypergeometric Function
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 571-578
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
Bounds for modified Bessel functions of the first and second kinds
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 575-599
-
- Article
-
- You have access
- Export citation
Erratum to: On Value Distribution Theory of Second Order Periodic ODEs, Special Functions and Orthogonal Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 2 / 01 April 2010
- Published online by Cambridge University Press:
- 20 November 2018, p. 261
- Print publication:
- 01 April 2010
-
- Article
-
- You have access
- Export citation
An Infinite Order Whittaker Function
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 2 / 01 April 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-381
- Print publication:
- 01 April 2009
-
- Article
-
- You have access
- Export citation
On Value Distribution Theory of Second Order Periodic ODEs, Special Functions and Orthogonal Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 4 / 01 August 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 726-767
- Print publication:
- 01 August 2006
-
- Article
-
- You have access
- Export citation
A limit theorem for the maxima of the para-critical simple branching process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 740-756
- Print publication:
- September 1998
-
- Article
- Export citation