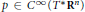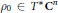2 results
trace and trace lifting theorems in weighted sobolev spaces
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 4 / Issue 4 / October 2005
- Published online by Cambridge University Press:
- 21 June 2005, pp. 509-552
- Print publication:
- October 2005
-
- Article
- Export citation
Semi-classical Integrability, Hyperbolic Flows and the Birkhoff Normal Form
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 5 / 01 October 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1034-1067
- Print publication:
- 01 October 2004
-
- Article
-
- You have access
- Export citation