Let  $\Gamma $ be a discrete group and let
$\Gamma $ be a discrete group and let 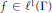 $f\,\in \,{{l}^{1}}(\Gamma )$. We observe that if the natural convolution operator
$f\,\in \,{{l}^{1}}(\Gamma )$. We observe that if the natural convolution operator 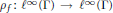 $\rho f\,:\,{{l}^{\infty }}(\Gamma )\,\to \,{{l}^{\infty }}(\Gamma )$ is injective, then
$\rho f\,:\,{{l}^{\infty }}(\Gamma )\,\to \,{{l}^{\infty }}(\Gamma )$ is injective, then 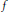 $f$ is invertible in
$f$ is invertible in 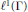 ${{l}^{1}}(\Gamma )$. Our proof simplifies and generalizes calculations in a preprint of Deninger and Schmidt by appealing to the direct finiteness of the algebra
${{l}^{1}}(\Gamma )$. Our proof simplifies and generalizes calculations in a preprint of Deninger and Schmidt by appealing to the direct finiteness of the algebra 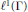 ${{l}^{1}}(\Gamma )$.
${{l}^{1}}(\Gamma )$.
We give simple examples to show that in general one cannot replace 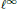 ${{l}^{\infty }}$ with
${{l}^{\infty }}$ with 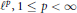 ${{l}^{p}},\,1\,\le \,p\,<\,\infty $, nor with
${{l}^{p}},\,1\,\le \,p\,<\,\infty $, nor with 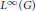 ${{L}^{\infty }}(G)$ for nondiscrete
${{L}^{\infty }}(G)$ for nondiscrete  $G$. Finally, we consider the problem of extending the main result to the case of weighted convolution operators on
$G$. Finally, we consider the problem of extending the main result to the case of weighted convolution operators on  $\Gamma $, and give some partial results.
$\Gamma $, and give some partial results.
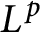 $L^p$
-algebras
$L^p$
-algebras
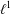 $\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
$\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS