5 results
Operators on Anti-dual pairs: Self-adjoint Extensions and the Strong Parrott Theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 813-824
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
ON THE EXTENSION OF ISOMETRIES BETWEEN THE UNIT SPHERES OF A
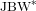 $\text{JBW}^{\ast }$-TRIPLE AND A BANACH SPACE
$\text{JBW}^{\ast }$-TRIPLE AND A BANACH SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 April 2019, pp. 277-303
- Print publication:
- January 2021
-
- Article
- Export citation
EXTENSIONS OF BOHR'S INEQUALITY
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 6 / December 2006
- Published online by Cambridge University Press:
- 19 December 2006, pp. 991-999
- Print publication:
- December 2006
-
- Article
- Export citation
EXTENSIONS OF POLYNOMIALS ON PREDUALS OF LORENTZ SEQUENCE SPACES
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue 2 / May 2005
- Published online by Cambridge University Press:
- 27 July 2005, pp. 395-403
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
Unique Hahn-Banach theorems for spaces of homogeneous polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-400
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation

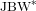
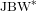


 (
(