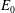 $E_{0}$-semigroup
$E_{0}$-semigroup
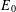 $E_{0}$-SEMIGROUPS ARE CONTINUOUS
$E_{0}$-SEMIGROUPS ARE CONTINUOUS
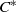 ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
 -Equation
-Equation