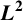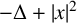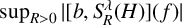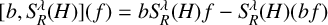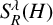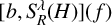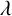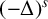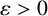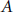13 results
A WEIGHTED
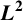 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 308-330
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
ON THE LOWEST EIGENVALUE OF THE FRACTIONAL LAPLACIAN FOR THE INTERSECTION OF TWO DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 02 December 2022, pp. 290-297
- Print publication:
- October 2023
-
- Article
- Export citation
Numerical Optimization and Noise Analysis of High-Tip-Speed Wind Turbine
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1461-1484
- Print publication:
- December 2017
-
- Article
- Export citation
Quasi boundary triples and semi-bounded self-adjoint extensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 895-916
- Print publication:
- October 2017
-
- Article
- Export citation
AN ATOMIC DECOMPOSITION FOR HARDY SPACES ASSOCIATED TO SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 125-144
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON A PERTURBED CONSERVATIVE SYSTEM OF SEMILINEAR WAVE EQUATIONS WITH PERIODIC-DIRICHLET BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 281-288
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
THE KATO SQUARE ROOT PROBLEM FOR MIXED BOUNDARY VALUE PROBLEMS
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 18 August 2006, pp. 113-130
- Print publication:
- August 2006
-
- Article
- Export citation
High Frequency Resolvent Estimates and Energy Decay of Solutions to the Wave Equation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 4 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 504-514
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
SOME HARDY-TYPE INEQUALITIES FOR THE GENERALIZED BAOUENDI-GRUSHIN OPERATORS
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 11 October 2004, pp. 515-527
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation
ON THE HIGH-ENERGY ASYMPTOTICS OF THE INTEGRATED DENSITY OF STATES
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 6 / November 2003
- Published online by Cambridge University Press:
- 08 October 2003, pp. 770-776
- Print publication:
- November 2003
-
- Article
- Export citation
Corrigendum to “Spectral Theory for the Neumann Laplacian on Planar Domains with Horn-Like Ends”
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 1 / 01 February 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
- Print publication:
- 01 February 2000
-
- Article
-
- You have access
- Export citation