2 results
Sufficiency of
$\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
$c$-cyclical monotonicity is the most important optimality condition for an optimal transport plan. While the proof of necessity is relatively easy, the proof of sufficiency is often more difficult or even elusive. We present here a new approach, and we show how known results are derived in this new framework and how this approach allows to prove sufficiency in situations previously not treatable.
Traceless Maps as the Singular Minimizers in the Multi-dimensional Calculus of Variations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 631-640
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
-
Let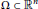
$\Omega \subset {{\mathbb{R}}^{n}}$ be a bounded Lipschitz domain and consider the energy functional1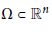
$$F[u,\Omega ]\,:=\,\,{{\int }_{\Omega }}\text{F}(\triangledown u(x))\,d\text{x,}$$over the space of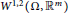
${{W}^{1,2}}(\Omega ,{{\mathbb{R}}^{m}})$ where the integrand 
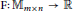$\text{F}:{{\mathbb{M}}_{m\times n}}\to \mathbb{R}$ is a smooth uniformly convex function with bounded second derivatives. In this paper we address the question of regularity for solutions of the corresponding system of Euler–Lagrange equations. In particular, we introduce a class of singularmaps referred to as traceless and examine themas a new counterexample to the regularity of minimizers of the energy functional 
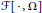$F[\cdot ,\Omega ]$ using a method based on null Lagrangians.
