For a partially multiplicative quandle (PMQ) ${\mathcal {Q}}$ we consider the topological monoid $\mathring {\mathrm {HM}}({\mathcal {Q}})$ of Hurwitz spaces of configurations in the plane with local monodromies in ${\mathcal {Q}}$. We compute the group completion of $\mathring {\mathrm {HM}}({\mathcal {Q}})$: it is the product of the (discrete) enveloping group ${\mathcal {G}}({\mathcal {Q}})$ with a component of the double loop space of the relative Hurwitz space $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$; here $G$ is any group giving rise, together with ${\mathcal {Q}}$, to a PMQ–group pair. Under the additional assumption that ${\mathcal {Q}}$ is finite and rationally Poincaré and that $G$ is finite, we compute the rational cohomology ring of $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$.

We study the degree of an L-Lipschitz map between Riemannian manifolds, proving new upper bounds and constructing new examples. For instance, if $X_k$ is the connected sum of k copies of $\mathbb CP^2$ for $k \ge 4$, then we prove that the maximum degree of an L-Lipschitz self-map of $X_k$ is between $C_1 L^4 (\log L)^{-4}$ and $C_2 L^4 (\log L)^{-1/2}$. More generally, we divide simply connected manifolds into three topological types with three different behaviors. Each type is defined by purely topological criteria. For scalable simply connected n-manifolds, the maximal degree is $\sim L^n$. For formal but nonscalable simply connected n-manifolds, the maximal degree grows roughly like $L^n (\log L)^{-\theta (1)}$. And for nonformal simply connected n-manifolds, the maximal degree is bounded by $L^\alpha $ for some $\alpha < n$.

We identify the cohomology of the stable classifying space of homotopy automorphisms (relative to an embedded disk) of connected sums of ${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$, where $3 \le k < l \le 2k - 2$. The result is expressed in terms of Lie graph complex homology.

This paper introduces a generalization of the $dd^c$-condition for complex manifolds. Like the $dd^c$-condition, it admits a diverse collection of characterizations, and is hereditary under various geometric constructions. Most notably, it is an open property with respect to small deformations. The condition is satisfied by a wide range of complex manifolds, including all compact complex surfaces, and all compact Vaisman manifolds. We show there are computable invariants of a real homotopy type which in many cases prohibit it from containing any complex manifold satisfying such $dd^c$-type conditions in low degrees. This gives rise to numerous examples of almost complex manifolds which cannot be homotopy equivalent to any of these complex manifolds.

The commutative differential graded algebra $A_{\mathrm {PL}}(X)$ of polynomial forms on a simplicial set $X$ is a crucial tool in rational homotopy theory. In this note, we construct an integral version $A^{\mathcal {I}}(X)$ of $A_{\mathrm {PL}}(X)$. Our approach uses diagrams of chain complexes indexed by the category of finite sets and injections $\mathcal {I}$ to model $E_{\infty }$ differential graded algebras (dga) by strictly commutative objects, called commutative $\mathcal {I}$-dgas. We define a functor $A^{\mathcal {I}}$ from simplicial sets to commutative $\mathcal {I}$-dgas and show that it is a commutative lift of the usual cochain algebra functor. In particular, it gives rise to a new construction of the $E_{\infty }$ dga of cochains. The functor $A^{\mathcal {I}}$ shares many properties of $A_{\mathrm {PL}}$, and can be viewed as a generalization of $A_{\mathrm {PL}}$ that works over arbitrary commutative ground rings. Working over the integers, a theorem by Mandell implies that $A^{\mathcal {I}}(X)$ determines the homotopy type of $X$ when $X$ is a nilpotent space of finite type.

We consider smooth, complex quasiprojective varieties $U$ that admit a compactification with a boundary, which is an arrangement of smooth algebraic hypersurfaces. If the hypersurfaces intersect locally like hyperplanes, and the relative interiors of the hypersurfaces are Stein manifolds, we prove that the cohomology of certain local systems on $U$ vanishes. As an application, we show that complements of linear, toric, and elliptic arrangements are both duality and abelian duality spaces.

Let $W$ be a compact simply connected triangulated manifold with boundary and let $K\,\subset \,W$ be a subpolyhedron. We construct an algebraic model of the rational homotopy type of $W\text{ }\!\!\backslash\!\!\text{ K}$ out of a model of the map of pairs $\left( K,\,K\cap \partial W \right)\,\to \,\left( W,\,\partial W \right)$ under some high codimension hypothesis.

We deduce the rational homotopy invariance of the configuration space of two points in a compact manifold with boundary under 2-connectedness hypotheses. Also, we exhibit nice explicit models of these configuration spaces for a large class of compact manifolds.

We study the germs at the origin of $G$-representation varieties and the degree 1 cohomology jump loci of fundamental groups of quasi-projective manifolds. Using the Morgan–Dupont model associated to a convenient compactification of such a manifold, we relate these germs to those of their infinitesimal counterparts, defined in terms of flat connections on those models. When the linear algebraic group $G$ is either $\text{SL}_{2}(\mathbb{C})$ or its standard Borel subgroup and the depth of the jump locus is 1, this dictionary works perfectly, allowing us to describe in this way explicit irreducible decompositions for the germs of these embedded jump loci. On the other hand, if either $G=\text{SL}_{n}(\mathbb{C})$ for some $n\geqslant 3$, or the depth is greater than 1, then certain natural inclusions of germs are strict.

In a previous work, we associated a complete differential graded Lie algebra to any finite simplicial complex in a functorial way. Similarly, we also have a realization functor fromthe category of complete differential graded Lie algebras to the category of simplicial sets. We have already interpreted the homology of a Lie algebra in terms of homotopy groups of its realization. In this paper, we begin a dictionary between models and simplicial complexes by establishing a correspondence between the Deligne groupoid of the model and the connected components of the finite simplicial complex.

In this short paper we try to describe the fundamental contribution of Quillen in the development of abstract homotopy theory and we explain how he uses this theory to lay the foundations of rational homotopy theory.

Let $X$ be an $n$-dimensional, finite, simply connected $\text{CW}$ complex and set

$${{\alpha }_{X}}\,=\,\underset{i}{\mathop{\lim \,\sup }}\,\frac{\log \,\text{rank}\,{{\pi }_{i}}\left( X \right)}{i}$$

When $0<{{\alpha }_{X}}<\infty $, we give upper and lower bounds for $\sum\nolimits_{i=k+2}^{k+n}{\,\text{rank}}\text{ }{{\pi }_{i}}\left( X \right)$ for $k$ sufficiently large. We also show for any $r$ that $\alpha x$ can be estimated from the integers $\text{rk }{{\pi }_{i}}\left( X \right),\,i\,\le \,nr$ with an error bound depending explicitly on $r$.

We study some basic properties of schematic homotopy types and the schematization functor. We describe two different algebraic models for schematic homotopy types, namely cosimplicial Hopf alegbras and equivariant cosimplicial algebras, and provide explicit constructions of the schematization functor for each of these models. We also investigate some standard properties of the schematization functor that are helpful for describing the schematization of smooth projective complex varieties. In a companion paper, these results are used in the construction of a non-abelian Hodge structure on the schematic homotopy type of a smooth projective variety.

We use Hodge theoretic methods to study homotopy types of complex projective manifolds with arbitrary fundamental groups. The main tool we use is the schematization functor, introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a Hodge decomposition on . This Hodge decomposition is encoded in an action of the discrete group on the object and is shown to recover the usual Hodge decomposition on cohomology, the Hodge filtration on the pro-algebraic fundamental group, and, in the simply connected case, the Hodge decomposition on the complexified homotopy groups. We show that our Hodge decomposition satisfies a purity property with respect to a weight filtration, generalizing the fact that the higher homotopy groups of a simply connected projective manifold have natural mixed Hodge structures. As applications we construct new examples of homotopy types which are not realizable as complex projective manifolds and we prove a formality theorem for the schematization of a complex projective manifold.

given an $n$-dimensional compact closed oriented manifold $m$ and a field $\mathbb k$, f. cohen and l. taylor have constructed a spectral sequence, ${\mathcal e}(m,n,\mathbb k)$, converging to the cohomology of the space of ordered configurations of $n$ points in $m$. the symmetric group $\sigma_n$ acts on this spectral sequence giving a spectral sequence of $\sigma_n$-differential graded commutative algebras. here, an explicit description is provided of the invariants algebra $(e_1,d_1)^{\sigma_n}$ of the first term of $\mathcal e(m,n,\mathbb q)$. this determination is applied in two directions.

(a) in the case of a complex projective manifold or of an odd-dimensional manifold $m$, the cohomology algebra $h^*(c_n(m);\mathbb q)$ of the space of unordered configurations of $n$ points in $m$ is obtained (the concrete example of $p^2(\mathbb c)$ is detailed).

(b) the degeneration of the spectral sequence formed of the $\sigma_n$-invariants $\mathcal e(m,n,\mathbb q)^{\sigma_n}$ at level 2 is proved for any manifold $m$.

these results use a transfer map and are also true with coefficients in a finite field $\mathbb f_p$ with $p>n$.

This paper contains a comparison of several definitions of equivariant formality for actions of torus groups. We develop and prove some relations between the definitions. Focusing on the case of the circle group, we use ${{S}^{1}}$ -equivariant minimal models to give a number of examples of ${{S}^{1}}$-spaces illustrating the properties of the various definitions.

Let P be a principal bundle with semisimple compact simply connected structure group G over a compact simply connected four-manifold M. In this paper we give explicit formulas for the rational homotopy groups and cohomology algebra of the gauge group and of the space of (irreducible) connections modulo gauge transformations for any such bundle.

We give conditions which determine if cat of a map go up when extending over a cofibre. We apply this to reprove a result of Roitberg giving an example of a 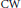$\text{CW}$ complex 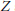$Z$ such that 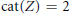$\text{cat}(Z)\,=\,2$ but every skeleton of 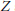$Z$ is of category 1. We also find conditions when 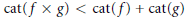$\text{cat}(f\,\times \,g)\,<\,\text{cat}(f)\,+\,\text{cat}(g)$. We apply our result to show that under suitable conditions for rational maps 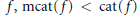$f,\,\text{mcat}(f)\,<\,\text{cat}(f)$ is equivalent to 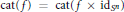$\text{cat(}f)\,=\,\text{cat(}f\,\times \,\text{i}{{\text{d}}_{{{S}^{n}}}})$. Many examples with 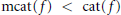$\text{mcat}(f)\,<\,\text{cat}(f)$ satisfying our conditions are constructed. We also answer a question of Iwase by constructing 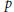$p$-local spaces 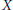$X$ such that 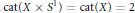$\text{cat(}X\ \times \,{{S}^{1}}\text{)}\,\text{=}\,\text{cat(}X\text{)}\,\text{=2}$. In fact for our spaces and every 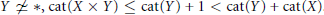$Y\,\not{\simeq }\,*,\,\text{cat}(X\,\times \,Y)\,\le \,\text{cat}(Y)\,+\,1\,\text{cat}(Y)\,+\,\text{cat}(X)$. We show that this same 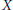$X$ has the property 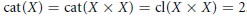$\text{cat}(X)=\,\text{cat}(X\,\times \,X)\,=\,\text{cl}(X\,\times \,X)\,=\,2$.

Soit $k$ un corps de caractéristique $p$ quelconque. Nous définissons la catégorie des $k$-algèbres de cochaînes fortement quasi-commutatives et nous donnons une condition nécessaire et suffisante pour que l’algèbre de cohomologie à coefficients dans ${{\text{Z}}_{2}}$ d’un objet de cette catégorie soit un module instable sur l’algèbre de Steenrod à coefficients dans ${{\text{Z}}_{2}}$.

A tout c.w. complexe simplement connexe de type fini $X$ on associe une $k$-algèbre de cochaînes fortement quasi-commutative; la structure de module sur l’algèbre de Steenrod définie sur l’algèbre de cohomologie de celle-ci coïncide avec celle de ${{H}^{*}}(X;\,{{\text{Z}}_{2}})$.

In this paper, we define the notion of ${{R}_{*}}\text{-LS}$ category associated to an increasing system of subrings of $\mathbb{Q}$ and we relate it to the usual $\text{LS}$-category. We also relate it to the invariant introduced by Félix and Lemaire in tame homotopy theory, in which case we give a description in terms of Lie algebras and of cocommutative coalgebras, extending results of Lemaire-Sigrist and Félix-Halperin.

LetM(X, Y) denote the space of all continuous functions between X and Y and Mƒ(X, Y) the path component corresponding to a given map ƒ : X → Y. When X and Y are classical flag manifolds, we prove the components of M(X, Y) corresponding to “simple” maps ƒ are classified up to rational homotopy type by the dimension of the kernel of ƒ in degree two cohomology. In fact, these components are themselves all products of flag manifolds and odd spheres.