Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T19:49:12.942Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ranks of the Homotopy Groups of a Finite Dimensional Complex

Published online by Cambridge University Press:  20 November 2018

Yves Félix ,
Steve Halperin  and
Jean-Claude Thomas
Yves Félix
Affiliation:
Université Catholique de Louvain 1348, Louvain-La-Neuve, Belgium, e-mail: felix@math.ucl.ac.be
Steve Halperin
Affiliation:
University of Maryland, College Park, MD 20742-3281, USA, e-mail: shalper@umd.edu
Jean-Claude Thomas
Affiliation:
CNRS.UMR 6093-Université d'Angers, 49045 Bd Lavoisier, Angers, France, e-mail: jean-claude.thomas@univ-angers.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 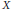$X$ be an 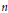$n$-dimensional, finite, simply connected 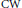$\text{CW}$ complex and set

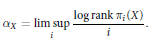$${{\alpha }_{X}}\,=\,\underset{i}{\mathop{\lim \,\sup }}\,\frac{\log \,\text{rank}\,{{\pi }_{i}}\left( X \right)}{i}$$

When 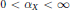$0<{{\alpha }_{X}}<\infty $, we give upper and lower bounds for 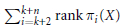$\sum\nolimits_{i=k+2}^{k+n}{\,\text{rank}}\text{ }{{\pi }_{i}}\left( X \right)$ for 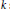$k$ sufficiently large. We also show for any 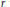$r$ that 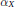$\alpha x$ can be estimated from the integers 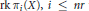$\text{rk }{{\pi }_{i}}\left( X \right),\,i\,\le \,nr$ with an error bound depending explicitly on 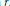$r$.

Keywords

55P3555P6217B70homotopy groupsgraded Lie algebraexponential growthLS category
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 1 , 01 February 2013 , pp. 82 - 119
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Adams, J. F. and Hilton, P. J., On the chain algebra of a loop space. Comment. Math. Helvetici. 30(1956), 305–330. http://dx.doi.org/10.1007/BF02564350 Google Scholar
[2]Anick, D. J., The smallest singularity of a Hilbert series. Math. Scand. 51(1982), no. 1, 35–44.Google Scholar
[3]Babenko, I. K., Analytical properties of Poincaré series of a loop space. Mat. Zametki. 27 (1980), no. 5, 751–765, 830.Google Scholar
[4] Félix, Y. and Halperin, S., Rational LS category and its applications. Trans. Amer. Math. Soc. 273(1982), no. 1, 1–38.Google Scholar
[5] Félix, Y., Halperin, S., and Thomas, J.-C., The homotopy Lie algebra for finite complexes. Inst. Hautes Études Sci. Publ. Math. 56(1983), 179–202.Google Scholar
[6] Thomas, J.-C., Rational homotopy theory. Graduate Texts in Mathematics, 205, Springer-Verlag, New York, 2001.Google Scholar
[7] Thomas, J.-C., Exponential growth and an asymptoptic formula for the ranks of homotopy groups of a finite1-connected complex. Ann. of Math. 170(2009), no. 1, 443–464. http://dx.doi.org/10.4007/annals.2009.170.443 Google Scholar
[8] Thomas, J.-C., Lie algebra of polynomial growth. J. London Math. Soc. 43(1991), no. 3, 556–566. http://dx.doi.org/10.1112/jlms/s2-43.3.556 Google Scholar
[9] Friedlander, J. and Halperin, S., An arithmetic characterization of the rational homotopy groups of certain spaces. Invent. Math. 53(1979), no. 2, 117–133. http://dx.doi.org/10.1007/BF01390029 Google Scholar
[10] Gelfand, I. M. and Kirillov, A. A., Sur les corps liés aux algèbres enveloppantes des algèbres de Lie. Inst. Hautes Études Sci. Publ. Math. 31(1966),5–19 Google Scholar
[11]Gottlieb, D., Evaluation subgroups of homotopy groups. Amer. J. Math. 91(1969), 729–756.http://dx.doi.org/10.2307/2373349 Google Scholar
[12]Halperin, S., Torsion gaps in the homotopy of finite complexes. II. Topology 30(1991), no. 3, 471–478. http://dx.doi.org/10.1016/0040-9383(91)90026-Z Google Scholar
[13]Krause, G. R. and Lenagan, T. H., Growth of algebras and Gel’fand-Kirillov dimension. Research Notes in Mathematics, 116, Pitman, Boston, MA, 1985.Google Scholar
[14] Lambrechts, P., Analytic properties of Poincaré series of spaces. Topology 37(1998), no. 6, 1363–1370. http://dx.doi.org/10.1016/S0040-9383(97)00083-9 Google Scholar
[15] Lambrechts, P., On the ranks of homotopy groups of two-cones. Topology Appl. 108(2000), no. 3, 303–314. http://dx.doi.org/10.1016/S0166-8641(99)00142-X Google Scholar
[16]Milnor, J. and Moore, J. C., On the structure of Hopf algebras. Annals of Math. 81(1965), 211–264. http://dx.doi.org/10.2307/1970615 Google Scholar
[17] van Lint, J. H. and Wilson, R.M., A course in combinatorics. Second ed., Cambridge University Press, Cambridge, 2001.Google Scholar