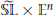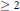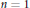7 results
Rigidity of flat holonomies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1048-1077
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 563-570
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicial complexity of surface groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 3153-3162
- Print publication:
- December 2020
-
- Article
- Export citation
INTERSECTIONS OF MULTICURVES FROM DYNNIKOV COORDINATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 149-158
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
On 3-manifolds with Torus or Klein Bottle Category Two
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-537
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Surgery on
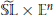 -Manifolds
-Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 2 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-287
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
Quaternions and Some Global Properties of Hyperbolic 5-Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 5 / 01 October 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1080-1099
- Print publication:
- 01 October 2003
-
- Article
-
- You have access
- Export citation




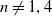

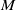
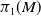
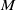

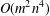
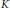
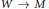
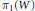
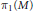
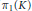
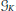
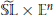 -Manifolds
-Manifolds