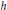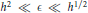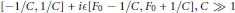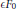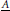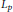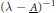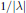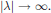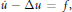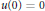3 results
Non-Selfadjoint Perturbations of Selfadjoint Operators in Two Dimensions IIIa. One Branching Point
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 3 / 01 June 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-657
- Print publication:
- 01 June 2008
-
- Article
-
- You have access
- Export citation
Semi-Classical Wavefront Set and Fourier Integral Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 2 / 01 April 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-263
- Print publication:
- 01 April 2008
-
- Article
-
- You have access
- Export citation
The Resolvent of Closed Extensions of Cone Differential Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 4 / 01 August 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 771-811
- Print publication:
- 01 August 2005
-
- Article
-
- You have access
- Export citation