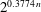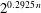In this paper we develop the theoretical foundations to exploit symmetries in modal logics. We generalize the notion of symmetries of propositional formulas in conjunctive normal form to modal formulas using the framework provided by coinductive modal models introduced in [5]. Hence, the results apply to a wide class of modal logics including, for example, hybrid logics. We present two graph constructions that enable the reduction of symmetry detection in modal formulas to the graph automorphism detection problem, and we evaluate the graph constructions on modal benchmarks.

In this paper, we present a heuristic algorithm for solving exact, as well as approximate, shortest vector and closest vector problems on lattices. The algorithm can be seen as a modified sieving algorithm for which the vectors of the intermediate sets lie in overlattices or translated cosets of overlattices. The key idea is hence no longer to work with a single lattice but to move the problems around in a tower of related lattices. We initiate the algorithm by sampling very short vectors in an overlattice of the original lattice that admits a quasi-orthonormal basis and hence an efficient enumeration of vectors of bounded norm. Taking sums of vectors in the sample, we construct short vectors in the next lattice. Finally, we obtain solution vector(s) in the initial lattice as a sum of vectors of an overlattice. The complexity analysis relies on the Gaussian heuristic. This heuristic is backed by experiments in low and high dimensions that closely reflect these estimates when solving hard lattice problems in the average case.

This new approach allows us to solve not only shortest vector problems, but also closest vector problems, in lattices of dimension $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n$ in time $2^{0.3774\, n}$ using memory $2^{0.2925\, n}$. Moreover, the algorithm is straightforward to parallelize on most computer architectures.

As models for molecular evolution, immune response, and local search algorithms, various authors have used a stochastic process called the evolutionary walk, which goes as follows. Assign a random number to each vertex of the infinite N-ary tree, and start with a particle on the root. A step of the process consists of searching for a child with a higher number and moving the particle there; if no such child exists, the process stops. The average number of steps in this process is asymptotic, as N → ∞, to log N, a result first proved by Macken and Perelson. This paper relates the evolutionary walk to a process called random bisection, familiar from combinatorics and number theory, which can be thought of as a transformed Poisson process. We first give a thorough treatment of the exact walk length, computing its distribution, moments and moment generating function. Next we show that the walk length is asymptotically normally distributed. We also treat it as a mixture of Poisson random variables and compute the asymptotic distribution of the Poisson parameter. Finally, we show that in an evolutionary walk with uniform vertex numbers, the ‘jumps’, ordered by size, have the same asymptotic distribution as the normalized cycle lengths in a random permutation.