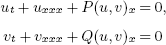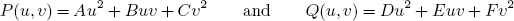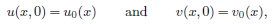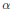6 results
Compatible finite element methods for geophysical fluid dynamics
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 291-393
-
- Article
-
- You have access
- Open access
- Export citation
Solving Two-Mode Shallow Water Equations Using Finite Volume Methods
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 5 / November 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1323-1354
- Print publication:
- November 2014
-
- Article
- Export citation
Global well-posedness for a system of KdV-type equations with coupled quadratic nonlinearities
-
- Journal:
- Nagoya Mathematical Journal / Volume 215 / September 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 67-149
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Global Well-Posedness and Convergence Results for the 3D-Regularized Boussinesq System
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 6 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1415-1435
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
A New Approach to Implement Sigma Coordinate in a Numerical Model
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1033-1050
- Print publication:
- October 2012
-
- Article
- Export citation
Fitting hidden semi-Markov models to breakpoint rainfall data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-157
- Print publication:
- 2001
-
- Article
- Export citation