In this paper we study the so-called random coeffiecient autoregressive models (RCA models) and (generalized) autoregressive models with conditional heteroscedasticity (ARCH/GARCH models). Both models can be represented as random systems with complete connections. Within this framework we are led (under certain conditions) to CL-regular Markov processes and we will give conditions under which (i) asymptotic stationarity, (ii) a law of large numbers and (iii) a central limit theorem can be shown for the corresponding models.

We show that if an input process ζ to a queue is asymptotic stationary in some sense, satisfies a condition AB and some other natural conditions, then the output processes (w, ζ) and (w, q,ζ) are asymptotic stationary in the same sense. Here, w and q are the waiting time and queue length processes, respectively.

An exponential approximation for the stationary waiting time distribution and the stationary queue size distribution for single-server queues in heavy traffic is given for a wide class of queues. This class contains for example not only queues for which the generic sequence, i.e. the sequence of service times and interarrival times, is stationary but also such queues for which the generic sequence is asymptotically stationary in some sense. The conditions ensuring the exponential approximation of the characteristics considered in heavy traffic are expressed in terms of the invariance principle for the stationary representation of the generic sequence and its first two moments.

The paper is a continuation of [7]. One of the main results is as follows: if the sequence (w, v, u) is asymptotically stationary in some sense then (l, w, v, u) is asymptotically stationary in the same sense. The other main result deals with an asymptotic behaviour of the vector of the queue size and the waiting time in the heavy-traffic situation. This result resembles a formula of the Little type.

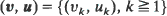The paper deals with the asymptotic behaviour of queues for which the generic sequence is not necessarily stationary but is asymptotically stationary in some sense. The latter property is defined by an appropriate type of convergence of probability distributions 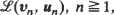of the sequences 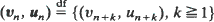to the distribution 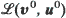of a stationary sequence 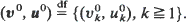We consider six types of convergence of 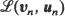to

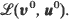
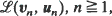The main result is as follows: if the sequence of the distributions converges in one of six ways then the sequence of distributions 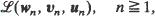of the sequences 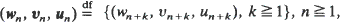converges in the same way, independently of initial conditions. Furthermore the limiting distribution is the same as the limiting distribution obtained by the weak convergence of the distributions 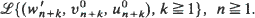Here wk and w∗k denote the waiting time of the kth unit in the queue generated by (v, u) and (v0, u0) respectively.

It is proved that, in a non-homogeneous Poisson cluster process whose cluster centre rate is λ(t), the long-term behaviour of several associated quantities is equivalent to their behaviour in a homogeneous process with centre rate Λ and the same cluster structure if λ(t)→ λ as t→∞.