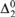Refine search
Actions for selected content:
28 results
INTROENUMERABILITY, AUTOREDUCIBILITY, AND RANDOMNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 December 2023, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIVERSAL CODING AND PREDICTION ON ERGODIC RANDOM POINTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 May 2022, pp. 387-412
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME QUESTIONS OF UNIFORMITY IN ALGORITHMIC RANDOMNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 12 August 2021, pp. 1612-1631
- Print publication:
- December 2021
-
- Article
- Export citation
A NOTE ON THE LEARNING-THEORETIC CHARACTERIZATIONS OF RANDOMNESS AND CONVERGENCE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 March 2021, pp. 807-822
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFINITE STRINGS AND THEIR LARGE SCALE PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 October 2020, pp. 585-625
- Print publication:
- June 2022
-
- Article
- Export citation
8 - Higher randomness
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 232-300
-
- Chapter
- Export citation
1 - Key developments in algorithmic randomness
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 1-39
-
- Chapter
- Export citation
6 - Aspects of Chaitin’s Omega
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 175-205
-
- Chapter
- Export citation
3 - Algorithmic randomness and constructive/computable measure theory
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 58-114
-
- Chapter
- Export citation
7 - Biased algorithmic randomness
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 206-231
-
- Chapter
- Export citation
2 - Algorithmic randomness in ergodic theory
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 40-57
-
- Chapter
- Export citation
5 - Relativization in randomness
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 134-174
-
- Chapter
- Export citation
4 - Algorithmic randomness and layerwise computability
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 115-133
-
- Chapter
- Export citation
9 - Resource bounded randomness and its applications
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 301-348
-
- Chapter
- Export citation
A LEARNING-THEORETIC CHARACTERISATION OF MARTIN-LÖF RANDOMNESS AND SCHNORR RANDOMNESS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 531-549
- Print publication:
- June 2021
-
- Article
- Export citation
RANK AND RANDOMNESS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 19 September 2019, pp. 1527-1543
- Print publication:
- December 2019
-
- Article
- Export citation
RANDOMNESS NOTIONS AND REVERSE MATHEMATICS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 09 September 2019, pp. 271-299
- Print publication:
- March 2020
-
- Article
- Export citation
GENERICITY AND RANDOMNESS WITH ITTMS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 09 September 2019, pp. 1670-1710
- Print publication:
- December 2019
-
- Article
- Export citation
ON THE INTERPLAY BETWEEN EFFECTIVE NOTIONS OF RANDOMNESS AND GENERICITY
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 393-407
- Print publication:
- March 2019
-
- Article
- Export citation
RANDOMNESS VIA INFINITE COMPUTATION AND EFFECTIVE DESCRIPTIVE SET THEORY
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 766-789
- Print publication:
- June 2018
-
- Article
- Export citation