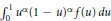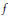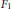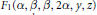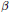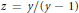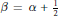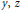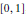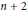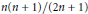Refine search
Actions for selected content:
1 results
Algebraic Evaluations of Some Euler Integrals, Duplication Formulae for Appell's Hypergeometric Function F 1, and Brownian Variations
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 5 / 01 October 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-981
- Print publication:
- 01 October 2000
-
- Article
-
- You have access
- Export citation
-
Explicit evaluations of the symmetric Euler integral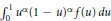
$\int _{0}^{1}\,{{u}^{\alpha }}{{(1-u)}^{\alpha }}f(u)\,du$ are obtained for some particular functions 
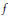$f$ . These evaluations are related to duplication formulae for Appell’s hypergeometric function 
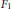${{F}_{1}}$ which give reductions of 
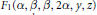${{F}_{1}}(\alpha ,\beta ,\beta ,2\alpha ,y,z)$ in terms of more elementary functions for arbitrary 
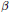$\beta $ with 
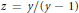$z=y/(y-1)$ and for 
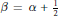$\beta =\alpha +\frac{1}{2}$ with arbitrary 
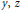$y,z$ . These duplication formulae generalize the evaluations of some symmetric Euler integrals implied by the following result: if a standard Brownian bridge is sampled at time 0, time 1, and at 
$n$ independent randomtimes with uniformdistribution on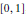 
$[0,1]$ , then the broken line approximation to the bridge obtained from these 
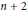$n+2$ values has a total variation whose mean square is 
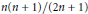$n(n+1)/(2n+1)$ .
