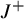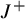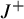In this paper, we introduce the notion of planar two-center Stark–Zeeman systems and define four
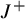 $J^{+}$
-like invariants for their periodic orbits. The construction is based on a previous construction for a planar one-center Stark–Zeeman system in [K. Cieliebak, U. Frauenfelder and O. van Koert. Periodic orbits in the restricted three-body problem and Arnold’s
$J^{+}$
-like invariants for their periodic orbits. The construction is based on a previous construction for a planar one-center Stark–Zeeman system in [K. Cieliebak, U. Frauenfelder and O. van Koert. Periodic orbits in the restricted three-body problem and Arnold’s
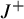 $J^+$
-invariant. Regul. Chaotic Dyn. 22(4) (2017), 408–434] as well as Levi-Civita and Birkhoff regularizations. We analyze the relationship among these invariants and show that they are largely independent, based on a new construction called interior connected sum.
$J^+$
-invariant. Regul. Chaotic Dyn. 22(4) (2017), 408–434] as well as Levi-Civita and Birkhoff regularizations. We analyze the relationship among these invariants and show that they are largely independent, based on a new construction called interior connected sum.
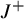 $J^+$
-invariants for planar two-center Stark–Zeeman systems
$J^+$
-invariants for planar two-center Stark–Zeeman systems