6 results
Further properties for unilateral binary processes
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue 2 / June 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 332-343
- Print publication:
- June 1982
-
- Article
- Export citation
Normal approximations for binary lattice systems
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 3 / September 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 674-685
- Print publication:
- September 1980
-
- Article
- Export citation
Ergodic properties of a two-dimensional binary process
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 1 / March 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 124-133
- Print publication:
- March 1980
-
- Article
- Export citation
Limiting results for arrays of binary random variables on rectangular lattices under sparseness conditions
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 3 / September 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 554-566
- Print publication:
- September 1979
-
- Article
- Export citation
An approximation to a two-dimensional binary process
-
- Journal:
- Journal of Applied Probability / Volume 14 / Issue 4 / December 1977
- Published online by Cambridge University Press:
- 14 July 2016, pp. 862-868
- Print publication:
- December 1977
-
- Article
- Export citation
On a two-dimensional binary process
-
- Journal:
- Journal of Applied Probability / Volume 13 / Issue 3 / September 1976
- Published online by Cambridge University Press:
- 14 July 2016, pp. 548-557
- Print publication:
- September 1976
-
- Article
- Export citation

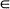
 The particular types of Markov random fields considered here provide clustering (or repulsion) alternatives to randomness and involve several parameters. The limiting results are used to consider statistical inference for these parameters. Finally, a simulation study is presented which examines the adequacy of the Poisson approximation and the inference techniques when the lattice dimensions are only moderately large.
The particular types of Markov random fields considered here provide clustering (or repulsion) alternatives to randomness and involve several parameters. The limiting results are used to consider statistical inference for these parameters. Finally, a simulation study is presented which examines the adequacy of the Poisson approximation and the inference techniques when the lattice dimensions are only moderately large.