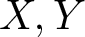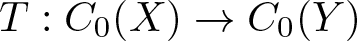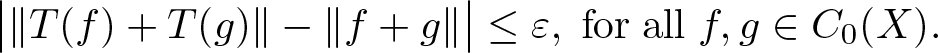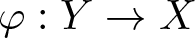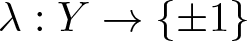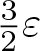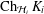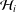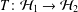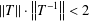Refine search
Actions for selected content:
3 results
Perturbations of norm-additive maps between continuous function spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1099-1114
-
- Article
- Export citation
SMALL-BOUND ISOMORPHISMS OF FUNCTION SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 412-429
- Print publication:
- December 2021
-
- Article
- Export citation
AN EXTENSION OF THE BANACH–STONE THEOREM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1-23
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation