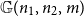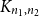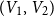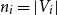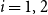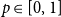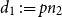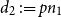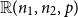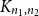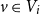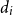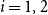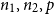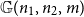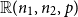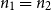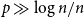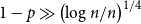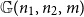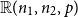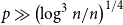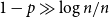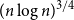Let
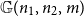 ${\mathbb{G}(n_1,n_2,m)}$
be a uniformly random m-edge subgraph of the complete bipartite graph
${\mathbb{G}(n_1,n_2,m)}$
be a uniformly random m-edge subgraph of the complete bipartite graph
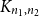 ${K_{n_1,n_2}}$
with bipartition
${K_{n_1,n_2}}$
with bipartition
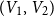 $(V_1, V_2)$
, where
$(V_1, V_2)$
, where
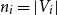 $n_i = |V_i|$
,
$n_i = |V_i|$
,
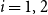 $i=1,2$
. Given a real number
$i=1,2$
. Given a real number
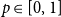 $p \in [0,1]$
such that
$p \in [0,1]$
such that
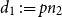 $d_1 \,{:\!=}\, pn_2$
and
$d_1 \,{:\!=}\, pn_2$
and
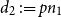 $d_2 \,{:\!=}\, pn_1$
are integers, let
$d_2 \,{:\!=}\, pn_1$
are integers, let
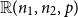 $\mathbb{R}(n_1,n_2,p)$
be a random subgraph of
$\mathbb{R}(n_1,n_2,p)$
be a random subgraph of
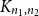 ${K_{n_1,n_2}}$
with every vertex
${K_{n_1,n_2}}$
with every vertex
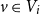 $v \in V_i$
of degree
$v \in V_i$
of degree
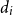 $d_i$
,
$d_i$
,
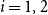 $i = 1, 2$
. In this paper we determine sufficient conditions on
$i = 1, 2$
. In this paper we determine sufficient conditions on
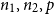 $n_1,n_2,p$
and m under which one can embed
$n_1,n_2,p$
and m under which one can embed
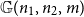 ${\mathbb{G}(n_1,n_2,m)}$
into
${\mathbb{G}(n_1,n_2,m)}$
into
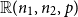 $\mathbb{R}(n_1,n_2,p)$
and vice versa with probability tending to 1. In particular, in the balanced case
$\mathbb{R}(n_1,n_2,p)$
and vice versa with probability tending to 1. In particular, in the balanced case
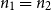 $n_1=n_2$
, we show that if
$n_1=n_2$
, we show that if
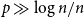 $p\gg\log n/n$
and
$p\gg\log n/n$
and
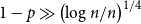 $1 - p \gg \left(\log n/n \right)^{1/4}$
, then for some
$1 - p \gg \left(\log n/n \right)^{1/4}$
, then for some
 $m\sim pn^2$
, asymptotically almost surely one can embed
$m\sim pn^2$
, asymptotically almost surely one can embed
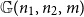 ${\mathbb{G}(n_1,n_2,m)}$
into
${\mathbb{G}(n_1,n_2,m)}$
into
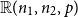 $\mathbb{R}(n_1,n_2,p)$
, while for
$\mathbb{R}(n_1,n_2,p)$
, while for
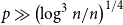 $p\gg\left(\log^{3} n/n\right)^{1/4}$
and
$p\gg\left(\log^{3} n/n\right)^{1/4}$
and
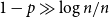 $1-p\gg\log n/n$
the opposite embedding holds. As an extension, we confirm the Kim–Vu Sandwich Conjecture for degrees growing faster than
$1-p\gg\log n/n$
the opposite embedding holds. As an extension, we confirm the Kim–Vu Sandwich Conjecture for degrees growing faster than
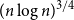 $(n \log n)^{3/4}$
.
$(n \log n)^{3/4}$
.