1 results
Heavy traffic limit theorems in fluctuation theory
-
- Journal:
- Advances in Applied Probability / Volume 10 / Issue 4 / December 1978
- Published online by Cambridge University Press:
- 01 July 2016, pp. 852-866
- Print publication:
- December 1978
-
- Article
- Export citation
-
Let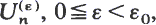
be a family of random walks with 
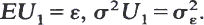For ε↓0 under certain conditions the random walk U(∊)n converges to an oscillating random walk. The ladder point distributions and expectations converge correspondingly. Let M∊ = max {U(∊)n, n ≧ 0}, v0 = min {n : U(∊)n = M∊}, v1 = max {n : U(∊)n = M∊}. The joint limiting distribution of ∊2σ∊–2v0 and ∊σ∊–2M∊ is determined. It is the same as for ∊2σ∊–2v1 and ∊σ–2∊M∊. The marginal ∊σ–2∊M∊ gives Kingman's heavy traffic theorem. Also lim ∊–1P(M∊ = 0) and lim ∊–1P(M∊ < x) are determined. Proofs are by direct comparison of corresponding probabilities for U(∊)n and for a special family of random walks related to MI/M/1 queues, using the central limit theorem.
be a family of random walks with 
For ε↓0 under certain conditions the random walk 