We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider a spatial point pattern realized from an inhomogeneous Poisson process on a bounded Borel set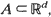 
, with intensity function λ (s; θ), where 
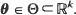. In this article, we show that the maximum likelihood estimator 
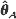and the Bayes estimator 
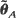are consistent, asymptotically normal, and asymptotically efficient as the sample region 
. These results extend asymptotic results of Kutoyants (1984), proved for an inhomogeneous Poisson process on [0, T]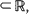 
, where T →∞. They also formalize (and extend to the multiparameter case) results announced by Krickeberg (1982), for the spatial domain 
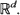. Furthermore, a Cramér–Rao lower bound is found for any estimator 
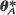of θ. The asymptotic properties of 
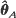and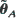 
are considered for modulated (Cox (1972)), and linear Poisson processes.
