Let $L:\Bbb R^N\times\Bbb R^N\rightarrow\Bbb R$ 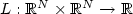be a Borelian function andconsider the following problems $$\inf\left\{F(y)=\int_a^bL(y(t),y'(t))\,{\rm d}t:\,y\in AC([a,b],\Bbb R^N), y(a)=A,\,y(b)=B\right\} \qquad\quad\! (P)$$ 
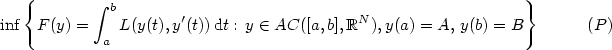 $$ \inf\left\{F^{**}(y)=\int_a^bL^{**}(y(t),y'(t))\,{\rm d}t:\,y\in AC([a,b],\Bbb R^N), y(a)=A,\,y(b)=B\right\}\cdot \quad\;\ \! (P^{**})$$ 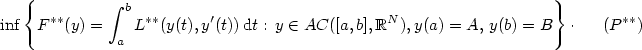We give a sufficient condition, weaker then superlinearity, under which $\inf F=\inf F^{**}$ if L is just continuous in x. We then extend a result of Cellina on the Lipschitz regularity of the minima of (P) when L is not superlinear.

We minimize, with respect to shape, the moment of inertia of a turbine having the given lowest eigenfrequency of the torsional oscillations. The necessary conditions of optimality in conjunction with certain physical parameters admit a unique optimal design.