1 results
Optimization of the anisotropic Cheeger constant with respect to the anisotropy
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1030-1043
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Given an open, bounded set
$\Omega $ in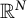 
$\mathbb {R}^N$, we consider the minimization of the anisotropic Cheeger constant 
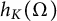$h_K(\Omega )$ with respect to the anisotropy K, under a volume constraint on the associated unit ball. In the planar case, under the assumption that K is a convex, centrally symmetric body, we prove the existence of a minimizer. Moreover, if 
$\Omega $ is a ball, we show that the optimal anisotropy K is not a ball and that, among all regular polygons, the square provides the minimal value.
