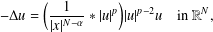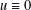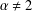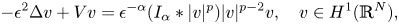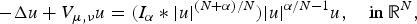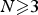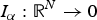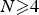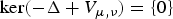5 results
Dual formulation of constrained solutions of the multi-state Choquard equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
- Export citation
Multiple bound states of higher topological type for semi-classical Choquard equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 329-355
- Print publication:
- February 2021
-
- Article
- Export citation
Groundstates for Choquard type equations with Hardy–Littlewood–Sobolev lower critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1377-1400
- Print publication:
- June 2020
-
- Article
- Export citation
Investigating the multiplicity and concentration behaviour of solutions for a quasi-linear Choquard equation via the penalization method
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 October 2015, pp. 23-58
- Print publication:
- February 2016
-
- Article
- Export citation