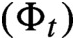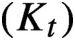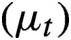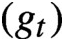6 results
EQUILIBRIUM STATES FOR CENTER ISOMETRIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 02 June 2023, pp. 1295-1355
- Print publication:
- May 2024
-
- Article
-
- You have access
- HTML
- Export citation
17 - Geometry and Dynamics of (All) Elliptic Functions
- from Part IV - Elliptic Functions: Classics, Geometry, and Dynamics
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 173-218
-
- Chapter
- Export citation
21 - Hausdorff and Packing Measures of Compactly Nonrecurrent Regular Elliptic Functions
- from Part VI - Compactly Nonrecurrent Elliptic Functions: Fractal Geometry, Stochastic Properties, and Rigidity
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 335-347
-
- Chapter
- Export citation
20 - Sullivan h-Conformal Measures for Compactly Nonrecurrent Elliptic Functions
- from Part VI - Compactly Nonrecurrent Elliptic Functions: Fractal Geometry, Stochastic Properties, and Rigidity
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 307-334
-
- Chapter
- Export citation
The conformal measures of a normal subgroup of a cocompact Fuchsian group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2845-2878
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
Loewner evolution of hedgehogs and 2-conformal measures of circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2734-2753
- Print publication:
- September 2021
-
- Article
- Export citation