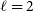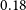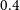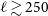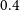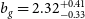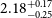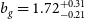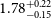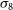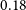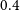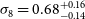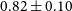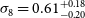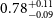Refine search
Actions for selected content:
6 results
Cross-correlating the EMU Pilot Survey 1 with CMB lensing: Constraints on cosmology and galaxy bias with harmonic-space power spectra
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 42 / 2025
- Published online by Cambridge University Press:
- 21 May 2025, e062
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extragalactic optical and near-infrared foregrounds to 21-cm epoch of reionisation experiments
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 12 / Issue S333 / October 2017
- Published online by Cambridge University Press:
- 08 May 2018, pp. 183-190
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Spatial distribution of the gamma-ray bursts at very high redshift
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 12 / Issue S333 / October 2017
- Published online by Cambridge University Press:
- 08 May 2018, pp. 203-206
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Towards an accurate model of redshift-space distortions: a bivariate Gaussian description for the galaxy pairwise velocity distributions
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 11 / Issue S308 / June 2014
- Published online by Cambridge University Press:
- 12 October 2016, pp. 340-341
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Tracing high redshift cosmic web with quasar systems
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 11 / Issue S308 / June 2014
- Published online by Cambridge University Press:
- 12 October 2016, pp. 161-166
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Giant radio galaxies and cosmic web
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 11 / Issue S308 / June 2014
- Published online by Cambridge University Press:
- 12 October 2016, pp. 484-485
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation