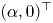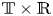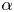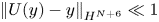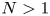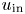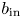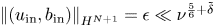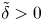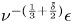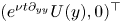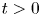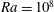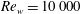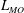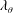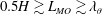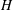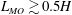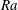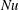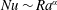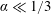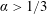In this work, we study the Sobolev stability of shear flows near Couette in the 2D incompressible magnetohydrodynamics (MHD) equations with background magnetic field $(\alpha,0 )^\top$ on $\mathbb {T}\times \mathbb {R}$. More precisely, for sufficiently large $\alpha$, we show that when the initial datum of the shear flow satisfies $\left \| U(y)-y\right \|_{H^{N+6}}\ll 1$, with $N>1$, and the initial perturbations ${u}_{\mathrm {in}}$ and ${b}_{\mathrm {in}}$ satisfy $\left \| ( {u}_{\mathrm {in}},{b}_{\mathrm {in}}) \right \| _{H^{N+1}}=\epsilon \ll \nu ^{\frac 56+\tilde \delta }$ for any fixed $\tilde \delta >0$, then the solution of the 2D MHD equations remains $\nu ^{-(\frac {1}{3}+\frac {\tilde \delta }{2})}\epsilon$-close to $( e^{\nu t \partial _{yy}}U(y),0)^\top$ for all $t>0$.

A viscous fluid is confined between two smooth horizontal walls, in a vertical channel. The upper wall may move with constant speed, but the lower wall is stationary and a portion of it is heated. A plume of heated fluid develops, and may also be swept downstream by the motion of the upper wall. When the heating effect is small and the upper plate does not move, a closed-form solution for the temperature profile is presented. A numerical spectral method is then presented, and allows highly accurate nonlinear solutions to be obtained, for the temperature and the fluid motion. These are compared against the closed-form solution in the linearized case, and the effects of nonlinearity on temperature and velocity are revealed. The results also show that periodic plume shedding from the heated region can occur in the nonlinear case.

We perform direct numerical simulations of wall sheared Rayleigh–Bénard convection for Rayleigh numbers up to 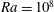$Ra=10^{8}$, Prandtl number unity and wall shear Reynolds numbers up to 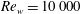$Re_{w}=10\,000$. Using the Monin–Obukhov length 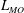$L_{MO}$ we observe the presence of three different flow states, a buoyancy dominated regime ($L_{MO}\lesssim \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$; with 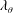$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$ the thermal boundary layer thickness), a transitional regime (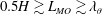$0.5H\gtrsim L_{MO}\gtrsim \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$; with 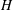$H$ the height of the domain) and a shear dominated regime (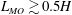$L_{MO}\gtrsim 0.5H$). In the buoyancy dominated regime, the flow dynamics is similar to that of turbulent thermal convection. The transitional regime is characterized by rolls that are increasingly elongated with increasing shear. The flow in the shear dominated regime consists of very large-scale meandering rolls, similar to the ones found in conventional Couette flow. As a consequence of these different flow regimes, for fixed 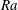$Ra$ and with increasing shear, the heat transfer first decreases, due to the breakup of the thermal rolls, and then increases at the beginning of the shear dominated regime. In the shear dominated regime the Nusselt number 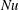$Nu$ effectively scales as 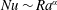$Nu\sim Ra^{\unicode[STIX]{x1D6FC}}$ with 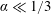$\unicode[STIX]{x1D6FC}\ll 1/3$, while we find $\unicode[STIX]{x1D6FC}\simeq 0.30$ in the buoyancy dominated regime. In the transitional regime, the effective scaling exponent is 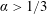$\unicode[STIX]{x1D6FC}>1/3$, but the temperature and velocity profiles in this regime are not logarithmic yet, thus indicating transient dynamics and not the ultimate regime of thermal convection.

Numerical instability may occur when simulating high Reynolds number flows by the lattice Boltzmann method (LBM). The multiple-relaxation-time (MRT) model of the LBM can improve the accuracy and stability, but is still subject to numerical instability when simulating flows with large single-grid Reynolds number (Reynolds number/grid number). The viscosity counteracting approach proposed recently is a method of enhancing the stability of the LBM. However, its effectiveness was only verified in the single-relaxation-time model of the LBM (SRT-LBM). This paper aims to propose the viscosity counteracting approach for the multiple-relaxation-time model (MRT-LBM) and analyze its numerical characteristics. The verification is conducted by simulating some benchmark cases: the two-dimensional (2D) lid-driven cavity flow, Poiseuille flow, Taylor-Green vortex flow and Couette flow, and three-dimensional (3D) rectangular jet. Qualitative and Quantitative comparisons show that the viscosity counteracting approach for the MRT-LBM has better accuracy and stability than that for the SRT-LBM.

Modelling fluid turbulence is perhaps one of the hardest problems in Applied Mathematics. In a recent paper, the author argued that the classical Navier–Stokes equation is not sufficient to describe the transition to turbulence, but that a Reiner–Rivlin type equation is needed instead. This is explored here for the simplest of all viscous fluid flows, the Couette flow, which is a simple shear between two moving plates. It is found that at high wavenumbers, the transition to unstable flow at the critical Reynolds number is characterized by a large number of eigenvalues of the Orr–Sommerfeld equation moving into the unstable zone essentially simultaneously. This would generate high-dimensional chaos almost immediately, and is a suggested mechanism for the transition to turbulence. Stability zones are illustrated for the flow, and a simple asymptotic solution confirms some of the features of these numerical results.

Hall effects on the unsteady Couette flow between two infinite horizontal parallel plates in a rotating system under the boundary layer approximations have been studied. One of the plate is at rest and the other oscillates in its own plane with the velocity U(t). An exact solution of the governing equations has been obtained by the use of the Laplace transform technique. The numerical results for the velocity components and the shear stresses are depicted graphically. Asymptotic behavior of the solution has analyzed for large values of magnetic parameter, rotation parameter and frequency parameter to gain some physical insight into the flow pattern. It is observed that there exists thin boundary layer (s) is formed near the stationary plate for large values of rotation parameter, magnetic parameter and frequency parameter.

The equilibrium position of a deformable drop in Couette and Poiseuille flows is investigated numerically by solving the full Navier-Stokes equations using a finite difference/front tracking method. The objective of this work is to study the motion of a non-neutrally buoyant drop in Couette and Poiseuille flows with different density ratios at finite Reynolds numbers. Couette flow: The equilibrium position of the lighter drops is higher than the heavier drops at each particle Reynolds number. Also, the equilibrium position height increases with increasing the Reynolds number at a fixed density ratio. At this equilibrium distance from the wall, the migration velocity is zero, while the velocity of the drop in the flow direction and rotational velocity of the drop is finite. It is observed that the equilibrium position is independent of the initial position of the drops and depends on the density ratio and the shear Reynolds number. Poiseuille flow: When the drop is slightly buoyant, it moves to an equilibrium position between the wall and the centerline. The equilibrium position is close to the centerline if the drop lags the fluid but close to the wall if the drop leads the fluid. As the Reynolds number increases, the equilibrium position of lighter drops moves slightly closer to the wall and the equilibrium position of heavier drops moves towards the centerline.