1 results
Generalized D-symmetric Operators II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-27
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation
-
Let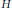
$H$ be a separable, infinite-dimensional, complex Hilbert space and let 
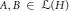$A,\,B\,\in \,\mathcal{L}\left( H \right)$, where 
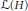$\mathcal{L}(H)$ is the algebra of all bounded linear operators on 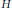$H$. Let 
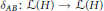${{\delta }_{AB}}\,:\mathcal{L}\left( H \right)\to \mathcal{L}\left( H \right)$ denote the generalized derivation 
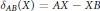${{\delta }_{AB}}\left( X \right)\,=\,AX\,-\,XB$. This note will initiate a study on the class of pairs 
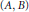$\left( A,\,B \right)$ such that 
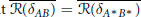$\overline{R\left( {{\delta }_{AB}} \right)}\,=\,\overline{R\left( {{\delta }_{A*\,B*}} \right)}$.
