1 results
A generalization of Bondy’s pancyclicity theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 554-563
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The bipartite independence number of a graph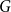
$G$, denoted as 
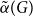$\tilde \alpha (G)$, is the minimal number 
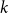$k$ such that there exist positive integers 
$a$ and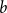 
$b$ with 
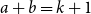$a+b=k+1$ with the property that for any two disjoint sets 
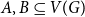$A,B\subseteq V(G)$ with 
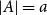$|A|=a$ and 
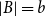$|B|=b$, there is an edge between 
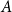$A$ and 
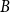$B$. McDiarmid and Yolov showed that if 
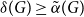$\delta (G)\geq \tilde \alpha (G)$ then 
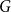$G$ is Hamiltonian, extending the famous theorem of Dirac which states that if 
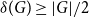$\delta (G)\geq |G|/2$ then 
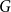$G$ is Hamiltonian. In 1973, Bondy showed that, unless 
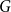$G$ is a complete bipartite graph, Dirac’s Hamiltonicity condition also implies pancyclicity, i.e., existence of cycles of all the lengths from 
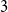$3$ up to 
$n$. In this paper, we show that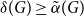 
$\delta (G)\geq \tilde \alpha (G)$ implies that 
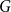$G$ is pancyclic or that 
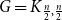$G=K_{\frac{n}{2},\frac{n}{2}}$, thus extending the result of McDiarmid and Yolov, and generalizing the classic theorem of Bondy.
