We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we study weak solutions, possibly unbounded and sign-changing, to the double phase problem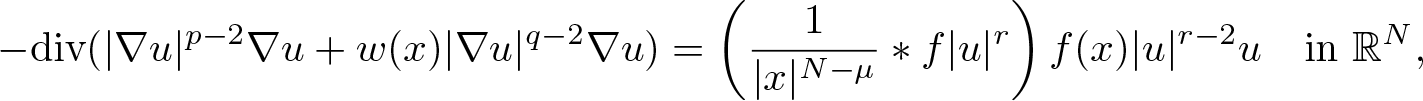where 
\begin{equation*}-\text{div} (|\nabla u|^{p-2} \nabla u + w(x)|\nabla u|^{q-2} \nabla u) = \left(\frac{1}{|x|^{N-\mu}}*f|u|^r\right) f(x)|u|^{r-2}u \quad\text{in}\ \mathbb{R}^N,\end{equation*}
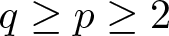$q\ge p\ge2$, r > q, 
$0 \lt \mu \lt N$ and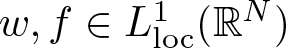 
$w,f \in L^1_{\rm loc}(\mathbb{R}^N)$ are two non-negative functions such that 
$w(x) \le C_1|x|^a$ and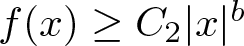 
$f(x) \ge C_2|x|^b$ for all 
$|x| \gt R_0$, where 
$R_0,C_1,C_2 \gt 0$ and 
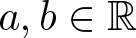$a,b\in\mathbb{R}$. Under some appropriate assumptions on p, q, r, µ, a, b and N, we prove various Liouville-type theorems for weak solutions which are stable or stable outside a compact set of 
$\mathbb{R}^N$. First, we establish the standard integral estimates via stability property to derive the non-existence results for stable weak solutions. Then, by means of the Pohožaev identity, we deduce the Liouville-type theorem for weak solutions which are stable outside a compact set.
