1 results
Extreme values and crossings for the X2-Process and Other Functions of Multidimensional Gaussian Processes, by Reliability Applications
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 3 / September 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 746-774
- Print publication:
- September 1980
-
- Article
- Export citation
-
Extreme values of non-linear functions of multivariate Gaussian processes are of considerable interest in engineering sciences dealing with the safety of structures. One then seeks the survival probability
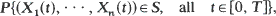
where X(t) = (X1(t), …, Xn(t)) is a stationary, multivariate Gaussian load process, and S is a safe region. In general, the asymptotic survival probability for large T-values is the most interesting quantity.
By considering the point process formed by the extreme points of the vector process X(t), and proving a general Poisson convergence theorem, we obtain the asymptotic survival probability for a large class of safe regions, including those defined by the level curves of any second- (or higher-) degree polynomial in (x1, …, xn). This makes it possible to give an asymptotic theory for the so-called Hasofer-Lind reliability index, β = inf>x∉S ||x||, i.e. the smallest distance from the origin to an unsafe point.
