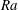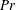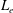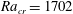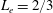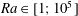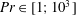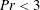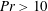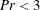Numerical simulations of thermoelectrohydrodynamic convection in a dielectric liquid inside a finite-length cylindrical annulus with a fixed temperature difference have been performed with increasing high-frequency electric tension under microgravity conditions. The electric field, coupled with the permittivity gradient, generates a dielectrophoretic buoyancy force whose non-conservative part can induce thermoelectric convection in the liquid. The liquid remains in a conductive state below a critical value of the applied electric voltage. At a critical value, a supercritical bifurcation occurs from the conductive state to a convective state made of stationary helicoidal vortices. A further increase of electric voltage leads to oscillatory helicoidal vortices and then to wavy patterns before spoke patterns dominate the convective flow. The dielectrophoretic force is shown to enhance the heat transfer from the hot to cold walls due to induced convective flows. Particularly, these results demonstrate that the dielectrophoretic buoyancy force holds promise to replace the gravitational force to induce efficient heat transfer in microgravity conditions, and they contribute to a better fundamental understanding of heat transfer in microgravity.

It is demonstrated how aqueous droplets with volumes down to the sub-femtolitre range can be manipulated, including the withdrawal of minute samples from the droplets. The underlying principle is that of partial coalescence with a liquid reservoir in an applied electric field. Upon partial coalescence, a droplet merges with a reservoir and reappears with a smaller diameter. The droplets studied here perform a reciprocating motion between two reservoirs during which their volume gets reduced. Manipulation of droplets with diameters down to 400 nm is reported. A similarity relation is derived expressing the ratio of droplet diameters before and after partial coalescence as a function of the ratio between electric and interfacial-tension forces. The presented scheme allows the withdrawal of minute samples from small droplets and could prove helpful in various applications where droplets are used as tiny reaction spaces or when the goal is to tailor the size of individual droplets.

Natural convection produced by a non-uniform internal heat source is studied numerically. Our investigation is limited to a two-dimensional enclosure with an aspect ratio equal to two. The energy source is Joule dissipation produced by an electric potential applied through two electrodes corresponding to a fraction of the vertical walls. The system of conservative equations of mass, momentum, energy and electric potential is solved assuming the Boussinesq approximation with a discontinuous Galerkin finite element method integrated over time. Three parameters are involved in the problem: the Rayleigh number 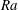$Ra$, the Prandtl number 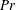$Pr$ and the electrode length 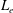$L_{e}$ normalized by the enclosure height. The numerical method has been validated in a case where electrodes have the same length as the vertical walls, leading to a uniform source term. The threshold of convection is established above a critical Rayleigh number, 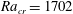$Ra_{cr}=1702$. Due to asymmetric boundary conditions on thermal field, the onset of convection is characterized by a transcritical bifurcation. Reduction of the size of the electrodes (from bottom up) leads to disappearance of the convection threshold. As soon as the electrode length is smaller than the cavity height, convection occurs even for small Rayleigh numbers below the critical value determined previously. At moderate Rayleigh number, the flow structure is mainly composed of a left clockwise rotation cell and a right anticlockwise rotation cell symmetrically spreading around the vertical middle axis of the enclosure. Numerical simulations have been performed for a specific 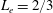$L_{e}=2/3$ with 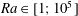$Ra\in [1;10^{5}]$ and 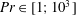$Pr\in [1;10^{3}]$. Four kinds of flow solutions are established, characterized by a two-cell symmetric steady-state structure with down-flow in the middle of the cavity for the first one. A first instability occurs for which a critical Rayleigh number depends strongly on the Prandtl number when 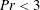$Pr<3$. The flow structure becomes asymmetric with only one steady-state cell. A second instability occurs above a second critical Rayleigh number that is quasiconstant when 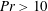$Pr>10$. The flow above the second critical Rayleigh number becomes periodic in time, showing that the onset of unsteadiness is similar to the Hopf bifurcation. When 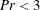$Pr<3$, a fourth steady-state solution is established when the Rayleigh number is larger than the second critical value, characterized by a steady-state structure with up-flow in the middle of the cavity.

A numerical scheme based on the immersed interface method (IIM) is developed to simulate the dynamics of an axisymmetric viscous drop under an electric field. In this work, the IIM is used to solve both the fluid velocity field and the electric potential field. Detailed numerical studies on the numerical scheme show a second-order convergence. Moreover, our numerical scheme is validated by the good agreement with previous analytical models, and numerical results from the boundary integral simulations. Our method can be extended to Navier-Stokes fluid flow with nonlinear inertia effects.

A nonlinear stability of two superposed semi-infinite Walters B′ viscoelastic dielectric fluids streaming through porous media in the presence of vertical electric fields in absence of surface charges at their interface is investigated in three dimensions. The method of multiple scales is used to obtain a Ginzburg-Landau equation with complex coefficients describing the behavior of the system. The stability of the system is discussed both analytically and numerically in linear and nonlinear cases, and the corresponding stability conditions are obtained. It is found, in the linear case, that the surface tension and medium permeability have stabilizing effects, and the fluid velocities, electric fields and kinematic viscoelastici-ties have destabilizing effects, while the porosity of porous medium and kinematic viscosities have dual role on the stability. In the nonlinear case, it is found that the fluid velocities, kinematic viscosities, kinematic viscoelasticities, surface tension and porosity of porous medium have stabilizing effects; while the electric fields and medium permeability have destabilizing effects.

A need exists to prolong the release of rapidly metabolized peptides of a low molecular weight, while delivering this peptide without environmental interference. Previous studies have used bovine serum albumin (BSA) as a model peptide to study release characteristics from alginate microcapsules. BSA is 66 kDa in size, while the peptide of interest here, connexin-43 carboxyl-terminus mimetic peptide (αCT1), is only 3.4 kDa. Such a change in size results in a much different set of release parameters. Our overall goal is a sustained release over a 24+ h period. Prolonged application of the peptide to a wound site to investigate therapeutic effects is ideal. As a result, a diffusion method using alginate microcapsules, along with the addition of poly-l-lysine and poly-l-ornithine, has been explored. We first aimed to establish and characterize our parameters through a set of parametric tests. Variations in polymer coating, change in pH, and changes in loading ratio have previously been shown to effect release using model compounds. Here we test specific changes in these parameters to show effects on the release of αCT1. Additionally, the microcapsules were attached to several biomaterials and surgical implants by ultraviolet cross-linking to study the effectiveness of attachment and delivery. Analysis and measurements using phase contrast microscopy, scanning electron microscopy, and atomic force microscopy were used to characterize changes in microcapsule morphology.

We propose and analyse two convergent fully discrete schemes to solve the incompressible Navier-Stokes-Nernst-Planck-Poisson system. The first scheme converges to weak solutions satisfying an energy and an entropy dissipation law. The second scheme uses Chorin's projection method to obtain an efficient approximation that converges to strong solutions at optimal rates.