We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the equation Δu = Vu in the half-space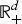 
${\open R}_ + ^d $, d ⩾ 2 where V has certain periodicity properties. In particular, we show that such equations cannot have non-trivial superexponentially decaying solutions. As an application this leads to a new proof for the absolute continuity of the spectrum of particular periodic Schrödinger operators. The equation Δu = Vu is studied as part of a broader class of elliptic evolution equations.
