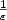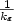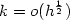The errors of an inertial navigation system (INS) in response to gyros' errors can be effectively reduced by the rotation technique, which is a commonly used method to improve an INS's accuracy. A gyro's error consists of a deterministic contribution and a stochastic contribution. The compensation effects of gyros' deterministic errors are clear now, but the compensation effects of gyros' stochastic errors are as yet unknown. However, the compensation effects are always needed in a rotational inertial navigation system's (RINS) error analysis and optimization study. In this paper, the compensation effects of gyros' stochastic errors, which are modelled as a Gaussian white (GW) noise plus a first-order Markov process, are analysed and the specific formulae are derived. During the research, the responses of an INS's and a RINS's position error equations to gyros' stochastic errors are first analysed. Then the compensation effects of gyros' stochastic errors brought by the rotation technique are discussed by comparing the error propagation characteristics in an INS and a RINS. In order to verify the theory, a large number of simulations are carried out. The simulation results show a good consistency with the derived formulae, which can indicate the correctness of the theory.

This paper studies the gradient flow of a regularized Mumford-Shah functionalproposed by Ambrosio and Tortorelli (1990, 1992) for image segmentation, and adopted by Esedoglu and Shen (2002) for image inpainting. It is shown that the gradient flow with L2 x L∞ initial data possesses a global weak solution, and it has a unique global in timestrong solution, which has at most finite number of point singularities in the space-time, when the initial data are in H1 x H1 ∩ L∞ . A family of fully discrete approximation schemes using low order finite elements is proposed for the gradient flow. Convergence of a subsequence (resp. the whole sequence)of the numerical solutions to a weak solution (resp. the strong solution) of the gradient flow is established as the mesh sizes tend to zero, and optimal and suboptimal order error estimates, which depend on $\frac{1}{{\varepsilon}}$ and $\frac{1}{k_{\varepsilon}}$ only in low polynomial order, are derived for the proposed fully discrete schemes under the mesh relation $k=o(h^{\frac12})$ . Numerical experiments are also presented to show effectiveness of the proposed numerical methods and to validate the theoretical analysis.