1 results
Asymptotic distributions for the Ehrenfest urn and related random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-356
- Print publication:
- September 1996
-
- Article
- Export citation
-
The distributions of nearest neighbour random walks on hypercubes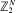
in continuous time t
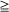0 can be expressed in terms of binomial distributions; their limit behaviour for t, N → ∞ is well-known. We study here these random walks in discrete time and derive explicit bounds for the deviation of their distribution from their counterparts in continuous time with respect to the total variation norm. Our results lead to a recent asymptotic result of Diaconis, Graham and Morrison for the deviation from uniformity for N →∞. Our proofs use Krawtchouk polynomials and a version of the Diaconis–Shahshahani upper bound lemma. We also apply our methods to certain birth-and-death random walks associated with Krawtchouk polynomials.
in continuous time 
0 can be expressed in terms of binomial distributions; their limit behaviour for 