This work characterizes the vanishing of the Fourier coefficients of all CM (Complex Multiplication) eta quotients. As consequences, we recover Serre’s characterization about that of $\eta(12z)^{2}$ and recent results of Chang on the pth coefficients of $\eta(4z)^{6}$ and $\eta(6z)^{4}$. Moreover, we generalize the results on the cases of weight 1 to the setting of binary quadratic forms.

Let f be a primitive Hilbert modular form over F of weight k with coefficient field $E_f$ , generated by the Fourier coefficients $C(\mathfrak {p}, f)$ for $\mathfrak {p} \in \mathrm {Spec}(\mathcal {O}_F)$ . Under certain assumptions on the image of the residual Galois representations attached to f, we calculate the Dirichlet density of $\{\mathfrak {p} \in \mathrm {Spec}(\mathcal {O}_F)| E_f = \mathbb {Q}(C(\mathfrak {p}, f))\}$ . For $k=2$ , we show that those assumptions are satisfied when $[E_f:\mathbb {Q}] = [F:\mathbb {Q}]$ is an odd prime. We also study analogous results for $F_f$ , the fixed field of $E_f$ by the set of all inner twists of f. Then, we provide some examples of f to support our results. Finally, we compute the density of $\{\mathfrak {p} \in \mathrm {Spec}(\mathcal {O}_F)| C(\mathfrak {p}, f) \in K\}$ for fields K with $F_f \subseteq K \subseteq E_f$ .

We prove that, given $2< p<\infty$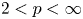, the Fourier coefficients of functions in $L_2(\mathbb {T}, |t|^{1-2/p}\,{\rm d}t)$ 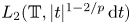belong to $\ell _p$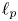, and that, given $1< p<2$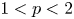, the Fourier series of sequences in $\ell _p$ 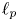belong to $L_2(\mathbb {T}, \vert {t}\vert ^{2/p-1}\,{\rm d}t)$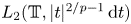. Then, we apply these results to the study of conditional Schauder bases and conditional almost greedy bases in Banach spaces. Specifically, we prove that, for every $1< p<\infty$ 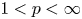and every $0\le \alpha <1$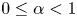, there is a Schauder basis of $\ell _p$ 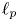whose conditionality constants grow as $(m^{\alpha })_{m=1}^{\infty }$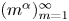, and there is an almost greedy basis of $\ell _p$ 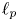whose conditionality constants grow as $((\log m)^{\alpha })_{m=2}^{\infty }$.

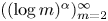Let F be a Siegel cusp form of degree $2$ , even weight $k \ge 2$ , and odd square-free level N. We undertake a detailed study of the analytic properties of Fourier coefficients $a(F,S)$ of F at fundamental matrices S (i.e., with $-4\det (S)$ equal to a fundamental discriminant). We prove that as S varies along the equivalence classes of fundamental matrices with $\det (S) \asymp X$ , the sequence $a(F,S)$ has at least $X^{1-\varepsilon }$ sign changes and takes at least $X^{1-\varepsilon }$ ‘large values’. Furthermore, assuming the generalized Riemann hypothesis as well as the refined Gan–Gross–Prasad conjecture, we prove the bound $\lvert a(F,S)\rvert \ll _{F, \varepsilon } \frac {\det (S)^{\frac {k}2 - \frac {1}{2}}}{ \left (\log \lvert \det (S)\rvert \right )^{\frac 18 - \varepsilon }}$ for fundamental matrices S.

We prove that if F is a nonzero (possibly noncuspidal) vector-valued Siegel modular form of any degree, then it has infinitely many nonzero Fourier coefficients which are indexed by half-integral matrices having odd, square-free (and thus fundamental) discriminant. The proof uses an induction argument in the setting of vector-valued modular forms. Further, as an application of a variant of our result and complementing the work of A. Pollack, we show how to obtain an unconditional proof of the functional equation of the spinor L-function of a holomorphic cuspidal Siegel eigenform of degree $3$ and level $1$ .

Let ${{\Theta }^{[j]}}$ be an analogue of the Ramanujan theta operator for Siegel modular forms. For a given prime $p$ , we give the weights of elements of mod $p$ kernel of ${{\Theta }^{[j]}}$ , where the mod $p$ kernel of ${{\Theta }^{[j]}}$ is the set of all Siegel modular forms $F$ such that ${{\Theta }^{[j]}}(F)$ is congruent to zero modulo $p$ . In order to construct examples of the mod $p$ kernel of ${{\Theta }^{[j]}}$ from any Siegel modular forms, we introduce new operators ${{A}^{(j)}}(M)$ and show the modularity of $F|{{A}^{\left( j \right)}}\left( M \right)$ when $F$ is a Siegel modular form. Finally, we give some examples of the mod $p$ kernel of ${{\Theta }^{[j]}}$ and the filtrations of some of them.

Let $A({{n}_{1}},\,{{n}_{2}},\ldots ,\,{{n}_{m}}-1)$ be the normalized Fourier coefficients of a Maass cusp form on $\text{GM(}m\text{)}$. In this paper, we study the cancellation of $A({{n}_{1}},\,{{n}_{2}},\ldots ,\,{{n}_{m}}-1)$ over Beatty sequences.

Recursive formulae satisfied by the Fourier coefficients of meromorphic modular forms on groups of genus zero have been investigated by several authors. Bruinier et al. [‘The arithmetic of the values of modular functions and the divisors of modular forms’, Compositio Math. 140(3) (2004), 552–566] found recurrences for SL(2,ℤ); Ahlgren [‘The theta-operator and the divisors of modular forms on genus zero subgroups’, Math. Res. Lett.10(5–6) (2003), 787–798] investigated the groups Γ0(p); Atkinson [‘Divisors of modular forms on Γ0(4)’, J. Number Theory112(1) (2005), 189–204] considered Γ0(4), and S. Y. Choi [‘The values of modular functions and modular forms’, Canad. Math. Bull.49(4) (2006), 526–535] found the corresponding formulae for the groups Γ+0(p). In this paper we generalize these results and find recursive formulae for the Fourier coefficients of any meromorphic modular form f on any genus-zero group Γ commensurable with SL(2,ℤ) , including noncongruence groups and expansions at irregular cusps. The form of the recurrence relations is well suited for the computation of the Fourier coefficients of the functions and forms on the groups which occur in monstrous and generalized moonshine. The required initial data has, in many cases, been computed by Norton (private communication).

For a general vector field we exhibit two Hilbert spaces, namely the space of so called closed functions and the space of exact functions and we calculate the codimension of the space of exact functions inside the larger space of closed functions. In particular we provide a new approach for the known cases: the Glauber field and the second-order Ginzburg–Landau field and for the case of the fourth-order Ginzburg–Landau field.

This paper describes a new approach to the parameterization of robot excitation trajectories for optimal robot identification. The trajectory parameterization is based on a combined Fourier series and polynomial functions. The coefficients of the Fourier series are optimized for minimal sensitivity of the identification to measurement disturbances, which is measured as the d-optimality criterion, taking into account motion constraints in joint and Cartesian space. This parameterization satisfies both the guarantees of convergence by adding terms and the matching of the boundary conditions. Application of the method for the identification of the CRS A465 industrial robot proves the validity of the proposed approach.