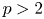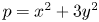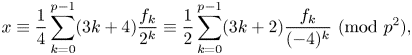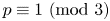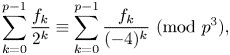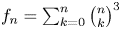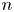1 results
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
- Export citation
-
In this paper, we mainly prove the following conjectures of Z.-W. Sun (J. Number Theory 133 (2013), 2914–2928): let p>2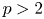 be a prime. If p=x^2+3y^2 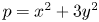with x,y\in \mathbb {Z} and x\equiv 1\ ({\rm {mod}}\ 3), then
x\equiv\frac14\sum_{k=0}^{p-1}(3k+4)\frac{f_k}{2^k}\equiv\frac12\sum_{k=0}^{p-1}(3k+2)\frac{f_k}{({-}4)^k}\ ({\rm{mod}}\ p^2),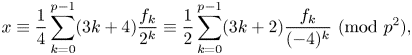and if p\equiv 1\pmod 3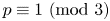, then\sum_{k=0}^{p-1}\frac{f_k}{2^k}\equiv\sum_{k=0}^{p-1}\frac{f_k}{({-}4)^k}\ ({\rm{mod}}\ p^3),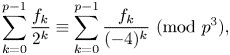where f_n=\sum _{k=0}^n\binom {n}k^3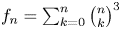 stands for the n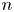th Franel number.
