In this paper, we study the twisted Ruelle zeta function associated with the geodesic flow of a compact, hyperbolic, odd-dimensional manifold X. The twisted Ruelle zeta function is associated with an acyclic representation 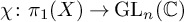 $\chi \colon \pi _{1}(X) \rightarrow \operatorname {\mathrm {GL}}_{n}(\mathbb {C})$, which is close enough to an acyclic, unitary representation. In this case, the twisted Ruelle zeta function is regular at zero and equals the square of the refined analytic torsion, as it is introduced by Braverman and Kappeler in [6], multiplied by an exponential, which involves the eta invariant of the even part of the odd-signature operator, associated with
$\chi \colon \pi _{1}(X) \rightarrow \operatorname {\mathrm {GL}}_{n}(\mathbb {C})$, which is close enough to an acyclic, unitary representation. In this case, the twisted Ruelle zeta function is regular at zero and equals the square of the refined analytic torsion, as it is introduced by Braverman and Kappeler in [6], multiplied by an exponential, which involves the eta invariant of the even part of the odd-signature operator, associated with 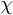 $\chi $.
$\chi $.