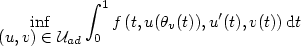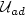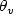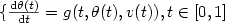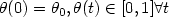1 results
How to state necessary optimality conditions for control problems with deviating arguments?
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 14 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 20 March 2008, pp. 381-409
- Print publication:
- April 2008
-
- Article
- Export citation
-
The aim of this paper is to give a general idea to state optimality conditions of control problems in the following form: ${\displaystyle\inf_{{\displaystyle(u,v)\in {\cal U}_{ad}}}\int_{0}^{1} f\left(t, u(\theta_v(t)),u^{\prime}(t),v(t)\right){\rm d}t}$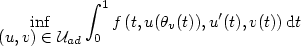
, (1)where ${\cal U}_{ad} $ 
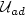is a set of admissible controls and $\theta_v$ 
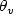is the solution of the following equation: $\{ \frac{{\rm d}\theta(t)}{{\rm d}t}=g(t,\theta(t),v(t)), t\in [0,1]$ 
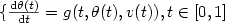; $\displaystyle\theta(0)=\theta_0, \theta(t)\in [0,1]\forall t$ 
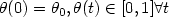. (2).The results are nonlocal and new.
