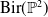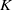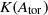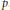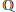8 results
Galois points and Cremona transformations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 471-478
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELEMENTARY EQUIVALENCE THEOREM FOR PAC STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 26 October 2020, pp. 1467-1498
- Print publication:
- December 2020
-
- Article
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Abelian varieties and Galois extensions of Hilbertian fields
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 16 May 2012, pp. 237-247
- Print publication:
- April 2013
-
- Article
- Export citation
Diamonds in Torsion of Abelian Varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 10 February 2010, pp. 477-480
- Print publication:
- July 2010
-
- Article
- Export citation
Oort groups and lifting problems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 849-866
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
Iterated Galois towers, their associated martingales, and the $p$-adic Mandelbrot set
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 20 September 2007, pp. 1108-1126
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Images of mod p Galois Representations Associated to Elliptic Curves
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-322
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation