The stability and control derivatives are essential parameters in the flight operation of aircraft, and their determination is a routine task using classical parameter estimation methods based on maximum likelihood and least-squares principles. At high angle-of-attack, the unsteady aerodynamics may pose difficulty in aerodynamic structure determination, hence data-driven methods based on artificial neural networks could be an alternative choice for building models to characterise the behaviour of the system based on the measured motion and control variables. This research paper investigates the feasibility of using a recurrent neural model based on an extreme learning machine network in the modelling of the aircraft dynamics in a restricted sense for identification of the aerodynamic parameters. The recurrent extreme learning machine network is combined with the Gauss–Newton method to optimise the unknowns of the postulated aerodynamic model. The efficacy of the proposed estimation algorithm is studied using real flight data from a quasi-steady stall manoeuvre. Furthermore, the estimates are validated against the parameters estimated using the maximum likelihood method. The standard deviations of the estimates demonstrate the effectiveness of the proposed algorithm. Finally, the quantities regenerated using the estimates present good agreement with their corresponding measured values, confirming that a qualitative estimation can be obtained using the proposed estimation algorithm.

We consider an iterated form of Lavrentiev regularization, using a null sequence (αk) of positive real numbers to obtain a stable approximate solution for ill-posed nonlinear equations of the form F(x)=y, where F:D(F)⊆X→X is a nonlinear operator and X is a Hilbert space. Recently, Bakushinsky and Smirnova [“Iterative regularization and generalized discrepancy principle for monotone operator equations”, Numer. Funct. Anal. Optim.28 (2007) 13–25] considered an a posteriori strategy to find a stopping index kδ corresponding to inexact data yδ with 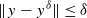resulting in the convergence of the method as δ→0. However, they provided no error estimates. We consider an alternate strategy to find a stopping index which not only leads to the convergence of the method, but also provides an order optimal error estimate under a general source condition. Moreover, the condition that we impose on (αk) is weaker than that considered by Bakushinsky and Smirnova.